lieu géométrique 2
-
Llouislegentleman dernière édition par
Bonjour,
J'ai un exercice sur le lieu géométrique. J'ai essayé de représenter le dessin mais je ne vois pas ce qu'on demande?
voici l'énoncé
Détermine le lieu géométrique des points tels que :
La distance de leurs projections orthogonales sur 2 droites perpendiculaires est constante
merci
-
mtschoon dernière édition par

Bonjour,
S'il s'agit de géométrie plane, je te joins un schéma pour t'éclairer.
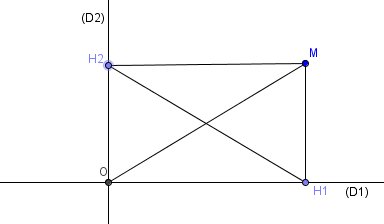
(D1) et (D2) sont les deux droites perpendiculaires se coupant en O.
M un point quelconque dont tu cherches le lieu
H1 et H2 sont les projetés de M sur (D1) et (D2)d étant un réel positif fixé, tu cherches l'ensemble des points M tels que H1H2=d
-
Llouislegentleman dernière édition par
le dessin me montre un rectangle dont H1H2 est une diagonale égale à la diagonale OM.
OM est par conséquent le rayon d'un cercle centré en O et de rayon OM donc d.L'équation de ce cercle serait alors x²+y² = d²
reste à le démontrer je suppose !!!
-
mtschoon dernière édition par

Tu as bien trouvé.
‘démontrer’ est un bien grand mot car les explications se ramènent à utiliser les propriétés des diagonales d’un rectangle.
Tout dépend de la rigueur exigée par ton professeur. A toi de voir (ici, on aide, mais on ne fait pas le travail à ta place !)
Tu peux raisonner par analyse-synthèse
Analyse : En prenant M un point quelconque du plan satisfaisant aux hypothèses, tu justifies que M est sur le cercle de centre 0 et de rayon d
Synthèse : En prenant un point M quelconque de ce cercle, tu justifies qu’il répond à la question (c’est à dire satisfait aux hypothèses de l’énoncé).
Ainsi, tu auras prouvé que le lieu de M est tout le cercle de centre 0 et de rayon d
Par contre, si tu veux donner l’équation cartésienne de ce cercle (cela ne me semble pas être demandé dans la question posée) il faut que tu définisses un repère, sinon l’équation n’a aucun sens.
Bon travail.
-
Llouislegentleman dernière édition par
Bonjour
Mon raisonnement suivant est il correct?Dans le repère orthonormé centré en (0,0)
Soit M (x,y) H1 (x,0) et H2 (0,y)H1H2 = d = √ x² + (-y)²
OM = √x² + y²(-y)² = y²
donc √ x² + (-y)² = √x² + y²
on peut donc affirmer que H1H2 = OM = d
donc pour supprimer la racine on peut élever au carréx² + y² = lOMl² = d²
soit l'équation d'un cercle centré en (0,0) et de rayon OM = dmerci
-
mtschoon dernière édition par

Cela me semble aller (si tu veux faire de l'analytique), mais précise mieux ton repère (o,u⃗,v⃗)(o,\vec{u},\vec{v})(o,u,v)
O point d'intersection de (D1) avec (D2)
u⃗\vec{u}u vecteur unitaire de (D1)
v⃗\vec{v}v vecteur unitaire de (D2)
-
Llouislegentleman dernière édition par
merci
J'ai un dernier exercice sur les lieux que je vais poster dans un nouveau message.
-
mtschoon dernière édition par

De rien.
D'accord.