Fonctions carrées (Parabole)

Bonsoir, voilà j'ai un petit exercice à faire et j'ai un petit problème :
voici le graphique :

La question est :
Résoudre graphiquement puis par le calcul h(x) supérieur ou égal à 1.

Graphiquement j'ai essayé ça :

On trace la droite d'équation y=1 et on lit les abscisses des points d'intersections de la droite avec la courbe. (j'hésite entre ->) S{ ]1;+ l'infini[ } (ou) S{-1;1;-2;2;-3;3;-4}

et par le calcul j'en ai aucune idée.

Merci de m'éclairer un peu plus.

Bonsoir,

Une autre fois, mets le graphique (voir Ajoute une image, en dessous du cadre texte, car c'est plus commode)

$fichier math$

Je ne comprends pas trop...
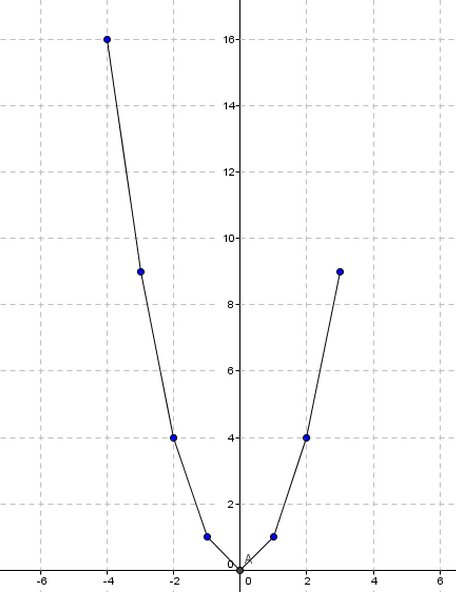
Cette "courbe" composée de 7 segments, est-elle donnée dans l'énoncé où est-ce toi qui l'a tracée ?
As-tu voulu représenter la parabole passant pas les points indiqués ? dans ce cas, la courbe est mauvaise et incomplète...

Merci de préciser.

Si tu as voulu tracerla parabole passant par les points, en lisant les abscisses des points de la parabole situés au-dessus de la droite d'équation y=1 (ou sur la droite d'équation y=1), l'ensemble des solutions cherché est ]-∞,-1] U [1,+∞[

elle est donnée par l'énoncé via un tableau de valeurs.

Ce ne serait pas ]-∞,-1[U]1,+∞[ ?

Si l'énoncé ne te donne qu'un tableau de valeurs, c'est donc toi qui a tracé la "dite" "courbe"...

Les crochets que tu proposes à -1 et 1 sont faux car tu as indiqué
Citation
h(x) supérieur
ou égalà 1

Les points correspondants ày=1(c'est-à-dire les points d'abscisses -1 et 1) font donc partie des solutions demandées.

Donc par le calcul c'est ça ?

$x2≥1x^2 \geq 1$
$x2−1≥0x^2-1 \geq 0$
$\geq 0$
$\geq 1$ ou $\leq -1$

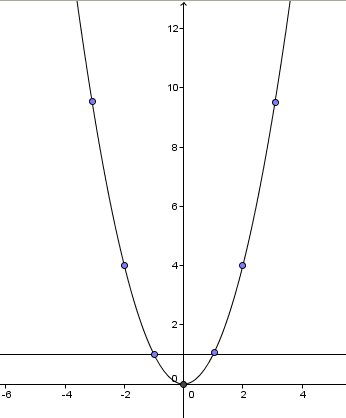
S'il s'agit de la parabole, représentation graphique de h définie par h(x)=x², je te joins le graphique exact.

$fichier math$

Par le calcul, c'est bon, mais en toute rigueur, tu dois faire un tableau pour le signe du produit (x-1)(x+1), avant tirer la conclusion.

D'accord j'en prendrai compte, car je suis épuisé je vais m'coucher, merci.

De rien ( et bonne nuit !)