Problème dans un triangle

[titi56fun]

Bonsoir, je bloque sur cet exercice pourriez-vous m'aider svp, merci pour votre aide

Exercice :
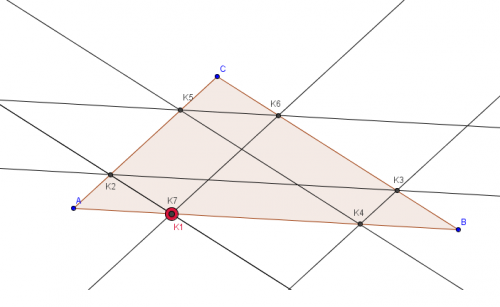
ABC est un triangle
K1 est un point de [AB]
Par K1 on trace D1 parallèles à (BC) ; D1 coupe [AC] en K2
Par K2 on trace D2 parallèles à (AB) ; D2 coupe [BC] en K3
etc.. on réitère ce processus indéfiniment.
Quelle conjecture peut-on faire ?

J'ai conjecturé que le point K1 ET K7 sont confondus mais je ne vois pas pourquoi ni comment justifier merci pour votre aide.

Voici ce que j'ai fais :

J'ai appliqué le théorème de Thalès donc sa donne sa :

AK1/AB = AK2/AC = BK3/BC = BK4/AB = CK5/CA = CK6/CB = AK7/AB

Mais maintenant je ne sais pas quoi faire, merci beaucoup

[mtschoon]

Bonjour,

Le théorème de Thalès semble convenir

$\frac{A{K}_1}{AB}=\frac{A{K}_2}{AC}=\frac{B{K}_3}{BC}=\frac{B{K}_4}{AB}=\frac{C{K}_5}{CA}=\frac{C{K}_6}{CB}=\frac{A{K}_7}{AB}$

Donc

$\frac{A{K}_1}{AB}=\frac{A{K}_7}{AB}$

Donc

$A{K}_1=A{K}_7$

$K_1$ est un point de [AB] donc les points K2,...,K7 sont sur les côtés du triangle ABC, donc K7 est un point de [AB] donc .....................

[titi56fun]

Bonjour, tout d'abord merci beaucoup pour votre réponse, mais je ne comprends pas la dernière phrase pourriez-vous svp m'expliquer si cela ne vous dérange pas merci beaucoup

[mtschoon]

$K_7$et $K_1$ sont sur le segment [AB], à distance égale de A (car $AK$_1$=A{K}_7$) donc il sont confondus.