Comment démontrer que des droites sont parallèles

Bonjour ,
Je bloque sur un exercice de vecteurs

Il faut que je démontre que les droites (DE) et (CF) sont ''parallèles'' → colinéaires

J'ai trouvé les coordonnées du points D et F

C=( 1 ; 0 )
D=( 1 ; 1 )
E=( 2,5 ; 2,5 )
F=( 0 ; 1/3 )

Le vecteur DE =
xE-xD = 2,5 – 1 = 1,5
yE-yD = 2,5 – 1 = 1,5

DE = ( 1,5 ; 1,5 )

Le vecteur CF =
xF-xC = 0 – 1 = -1
yF-yC = 1/3 -0 = 1/3

CF = ( -1 ; 1/3 )

Si les vecteurs DE et CF sont colinéaires , alors les droites sont parallèles

Sauf que je n'arrive pas à trouver le réel k qui les font colinéaires

Merci de m'aider

Bonjour,
Tes deux vecteurs ne sont pas colinéaires.
Donne l'énoncé depuis le début afin que l'on puisse vérifier les coordonnées de tes points.

Enoncé :

Soit ABC un triangle et O le milieu de [ BC ]

On définit les points D , E et F par :

AD = AB + AC

DE = AO + BC

AF = 1/3AB

Faire un figure
Dans le repère ( A ; B ; C ) , déterminer les coordonnées des points :
B , C , O ,D , E et F
Démontrer que les droites ( DE ) et ( CF ) sont parallèles

Mes réponses :

B = ( 0;1 )
C = ( 1 ; 0)
0 = ( 0,5 ; 0,5 )
D = ( 1 ; 1 )
E = ( 2,5 ; 2,5 )
F = ( 0 ; 1/3 )

Pour trouver D :

xD - xA = xB – xA + xC – xA = 0 – 0 + 1 – 0 = 1
yD – yA = yB – yA + yC – yA = 1 – 0 + 0 – 0 = 1

xD – 0 = 1
xD = 1

yD – 0 = 1
yD = 1

Pour trouver E :

xE – xD = xO – xA + xC – xB = 0,5 – 0 + 1 – 0 = 1,5
yE – yD = yO – yA + yC – yB = 0,5 – 0 + 0 – 1 = 1,5

xE - 1 = 1,5
xE = 2,5

yE – 1 = 1,5
yE = 2,5

Pour trouver F :

xF – xA = 1/3 * ( xB - xA sur yB - yA)
= 1/3 * ( 0 - 0 sur 1 - 0 )
= 1/3 * ( 0 ; 1 )
= 1/3 * sur 1/3*1
= 0
1/3

xF - xA = 0
yF – yA = 1/3

xF – 0 = 0
xF = 0

yF – 0 = 1/3
yF = 1/3

Si le repère est (A ; B ; C), les coordonnées de B sont (1 ; 0) et celles de C sont ( 0 ; 1) et non l'inverse.

Ah d'accord
Donc b = ( 1 ; 0 ) et c = ( 0 ; 1 )

Oui, mais tu dois avec cela recalculer les coordonnées de tes points O, D, E, et F. Puis celles des vecteurs DE et CF.

B =( 1 ; 0 )
C = ( 0 ; 1)
0 = ( 0,5 ; 0,5 )

Pour trouver D :

xD - xA = xB – xA + xC – xA = 1 – 0 + 0 – 0 = 1
yD – yA = yB – yA + yC – yA = 0 – 0 + 1 – 0 = 1

xD – 0 = 1
xD = 1

yD – 0 = 1
yD = 1

Donc D=(1;1) ???

Pour trouver E :

xE – xD = xO – xA + xC – xB = 0,5 – 0 + 0 –1 = -0,5
yE – yD = yO – yA + yC – yB = 0,5 – 0 + 1 – 0 = 1,5

xE - 1 = 0,5
xE = 0,5

yE – 1 = 1,5
yE = 2,5

Donc E = ( 0,5 ; 2,5) ???

Pour trouver F :

xF – xA = 1/3 * ( xB - xA sur yB - yA)
= 1/3 * ( 1 - 0 sur 0 - 0 )
= 1/3 * ( 1 ; 0 )
= 1/3 * 1 sur 1/3*0
= 1/3 sur 0

xF - xA = 1/3
yF – yA = 0

xF – 0 = 1/3
xF = 1/3

yF – 0 = 0
yF = 0

Donc F = ( 1/3 ; 0 )

Mais je trouve toujours pas que DE est colinéaire avec CF

car DE = -0,5 sur 1,5
et CF = 1/3 sur -1

car
-0,5 = 1/3
1,5 = -1

donc je fais -1*1,5 = 1,5 et 1/3 * 1,5 = 0,5 et non -0,5

Tes notations sont bizarres.
Que veux-tu dire par "sur" ?
De plus tu écris -0,5 = 1/3 et 1,5 = -1 qui sont évidemment fausses.
Utilise les couples, par exemple, DE = (-0,5 ; 1,5) et CF = (1/3 ; -1) (il s'agit bien sûr des vecteurs).
Et non pas "sur".
Maintenant, regarde les produits en croix, en faisant attention aux signes.

DE = ( -0,5 ; 1,5 )
CF = ( 1/3 ; -1 )

Pour savoir si les vecteurs sont parallèles , donc colinéaires , il faut trouver un réel M tel tel que par exemple le vecteur u = M* vecteur v

donc DE = -1,5*CF car ( -1,5 * 1/3 ; -1,5 * -1 ) = ( -0,5 ; 1 ,5 ) = DE

donc ils sont parallèles

Tes calculs sont justes, mais tu confonds vecteurs et droites.
Les vecteurs sont colinéaires, pas "parallèles".
Les droites (DE) et (CF) sont peut-être parallèles.
Pourquoi "peut-être" ?
Parce que si les vecteurs DE et CF sont colinéaires, les droites (DE) et (CF) sont parallèles ou confondues.
Tu dois t’assurer que ces droites ne sont pas confondues.
Comment, en comparant, par exemple, les vecteurs DE et DC.

je ne comprends pas pourquoi il faudrait cmparé les droites DE et DC puisqu'à l'oeil nu on peut voir que les vecteurs DE et CF ne sont pas confondues

je ne comprends pas pourquoi il faudrait cmparé les droites DE et DC puisqu'à l'oeil nu on peut voir que les vecteurs DE et CF ne sont pas confondues

Encore une fois, tu confonds droite et vecteur !
"A l’œil nu", cela n'est pas une démonstration.
On fait des Maths, pas des sciences expérimentales.

Si je fais une figure

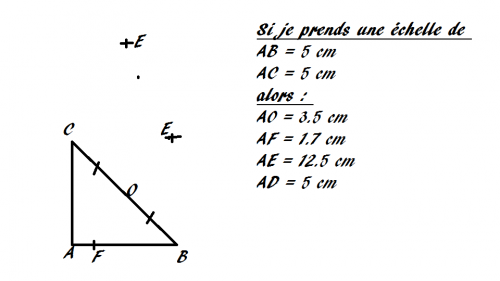
$fichier math$

pour revenir sur les droites - vecteurs

comment on peux comparerles vecteurs DE et DC ?

Attention : sur ta figure il y a deux points E. Je présume que le plus bas est en fait le point D.
Tu as déjà les coordonnées du vecteur DE : (-0.5 ; 1.5).
Connaissant les coordonnées de D et de C, tu obtiens aisément celles du vecteur DC.
D = (1 ; 1) et C = (0 ; 1). D'où DC.

Donc DC = ( -1 ; 1 ) et DE = ( -0.5 ; 1.5 )
ce qui m’amène à ?

DC est faux.
Après correction, regarde si ces deux vecteurs sont colinéaires ou pas.
S'ils le sont, C est sur la droite (DE), et donc les droites (DE) et (CF) sont confondues.
Sinon, C n'est pas sur la droite (DE), et les droites (DE) et (CF) sont parallèles.

Donc pour répondre à la question : démontrer que les droites ( DE ) et ( CF ) sont parallèles
je réponds que comme les vecteurs DE et CF sont colinéaires et que C n'appartient pas à la droite ( DE ) , alors les droites ( DE ) et ( CF ) sont parallèles

DC = ( -1 ; 0 ) ?

Oui.
Maintenant que tu as corrigé DC, vérifie que les vecteurs DC et DE ne sont pas colinéaires afin de justifier que C n'appartient pas à la droite (DE).