DM sur la trigonométrie - seconde

figure triangle

bonjour, j'ai un dm sur la trigonométrie avec α et β, je vous met les questions ainsi que les réponses, pourriez vous me dire si j'ai bon ou pas? merci d'avance PS : la figure est au dessus (le lien)

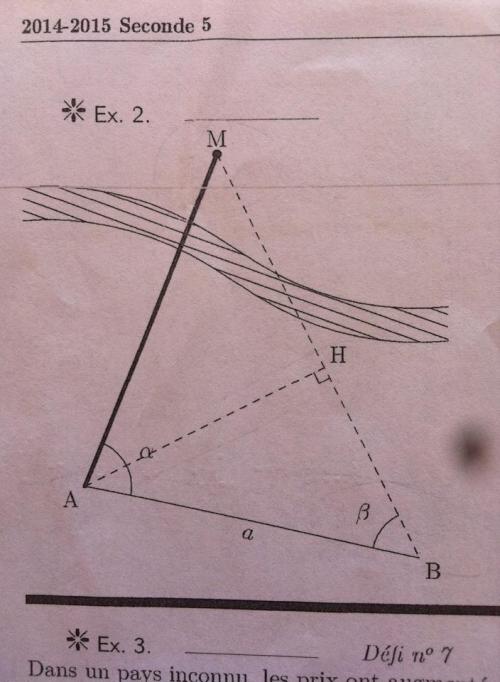
"A l'aide de la figure ci-dessus, on cherche à déterminer la longueur AM du point M visible de A et B. Les données connues sont indiquées sur la figure : AB = a ; l'angle MAB = α et l'angle ABM = β. Dans le triangle ABM, H est le pied de la hauteur issue de A.

On appelle ϒ l'angle AMB. Exprimeϒ en fonction de α et β.
a_ Exprime la longueur AH en fonction de AB et β.

b_ Exprime la longueur AH en fonction de AM et ϒ.

Déduis-en la formule qui permet de calculer AM en fonction de AB, α et β."

Voici mes réponses :

je n'ai rien mis car je ne comprend pas
a_ sin β = AH/AB

sin β = α/a

α = sin β x a

b_ sin ϒ = AH/AM

sin ϒ = α/AM

α = sin ϒ x AM
3) je n'ai pas trouvé la formule

Pourriez vous m'aider pour la 1) et la 3) et me dire si j'ai bon ou pas aux autres questions? merci d'avance

Bonjour,

Pistes,

Tu n'indiques pas quel est l'unité d'angle .

La somme des angles d'un triangle vaut ∏ radians , c'est à dire 180°

Si l'unité d'angle est le radian, α+β+γ=∏ doncγ=∏-(α+β)

Adapte si l'unité n'est pas le radian.

Pour la 2), je n'ai pas bien compris tes écritures...

$sin⁡β=AHAB\sin\beta=\frac{AH}{AB}$ donc $AH=ABsinβAH=ABsin\beta$

$sin⁡γ=AHAM\sin\gamma=\frac{AH}{AM}$ donc $AH=AMsinγAH=AMsin\gamma$

Pour la 3), tu peux déduire du 2) que :

$ABsinβ=AMsinγABsin\beta=AMsin\gamma$

Tu isoles AM, puis tu remplaces γ par l'expression trouvée au 1) et tu simplifies au mieux.

bonjour, merci d'avoir répondu
Sur ma feuille, on indique pas l'unité d'angle mais c'est forcément le dégré puisqu'on n'a jamais parlé de radian. Du coup, ça change quoi que ça soit en radian ou en degré ?

Merci pour la 3) mais justement je ne trouve pas l'expression du 1)... peux tu m'aider stp ?

et pourquoi je dois isolé AM ?

Vu que tu ne connais pas les radians, de sont les degrés qui sont utilisés.

Pour la 1), tu dois savoir que la somme des angles d'un triangle vaut 180°

Donc, les angles étant exprimés en degrés, dans le triangle AMB :

α+β+γ=180 donc γ=180-(α+β)

Pour la 3), l'énoncé dit :
Citation
calculer AM en fonction de AB, α et β

Il faut donc que tu trouves AM = ....

C'est ce que j'ai appelé "isoler AM "

j'ai trouvé, j'ai mis ça :
comme AH = a x $sin⁡(β)\sin \left(\beta \right)$
et AH = AM x $sin⁡(γ)\sin \left(\gamma \right)$
, alors a x $sin⁡(β)\sin \left(\beta \right)$ = AM x $sin⁡(γ)\sin \left(\gamma \right)$

ensuite : $a∗sin⁡(γ)sin⁡γ\frac{a*\sin \left(\gamma \right)}{\sin \gamma }$ = AM

les $sin⁡(γ)\sin \left(\gamma \right)$ s'annulent, on a donc : AM = a

normalement c'est bon

La fin de tes calculs n'est pas bonne car tu fais des confusions entre les angles.

$sin\gamma=a\sin\beta$

Donc $AM=asin⁡βsin⁡γAM=a\frac{\sin\beta}{\sin\gamma}$

Ensuite, comme je te l'ai déjà indiqué, tu remplaces γ par l'expression trouvée à la 1)

donc ça donne : $a\frac{\sin \left(\beta \right)}{\sin \left(180-\alpha -\beta \right)}$
c'est bien ca ?

Oui, c'est bien ça.

Si tu connais les propriétés desangles supplémentaires, tu peux simplifier un peu.

$sin⁡(180−x)=sin⁡x\sin(180-x)=\sin x$

Ainsi, tu peux obtenir :

$AM=asin⁡βsin⁡(α+β)AM=a\frac{\sin\beta}{\sin(\alpha+\beta)}$

Si tu ne connais pas, tu conserves l'expression précédente.

je comprends pas d'où vient : $sin⁡(180−x)=sin⁡x\sin \left(180-x \right) = \sin x$
donc je comprends pas comment on obtient : $a\frac{\sin (\beta) }{\sin \left(\alpha +\beta \right)}$

je viens de comprendre d'où vient la 2eme expression mais pas la 1ere..

C'est du cours : 180-x et x sont des mesures d'angles supplémentaires ( leur somme vaut 180°)

$sin⁡(180−x)=sin⁡x\sin(180-x)=\sin x$ est la propriété des sinus d'angles supplémentaires : J'ignore si tu connais cette propriété...

Comme je te l'ai déjà dit, si tu ne la pas vu en cours, tu ne l'utilises pas et tu conserves la formule précédente de AM.

Excuse de revenir, mais je voulais savoir si on pouvait développer $a\frac{\sin \left(\beta \right)}{\sin \left(\alpha +\beta \right)}$ ou est-ce que je laise ca comme ca pcq je n'arrive pas à la développer sinon..

Evidemment, avec les formules d'addition (1S) tu pourrais developper le dénominateur mais je pense que tu ne les connais pas et de plus, ça ne servirait à rien.

Donc, tu laisses ainsi.

Ah non c'est en première qu'on voit ca donc je connais pas mais du coup ca vaudrait pas mieux que je garde ce que j'avais fait en arrivant a la fin à AM = a comme ca j'ai au moins un résultat

L'énoncé te demande :
Citation
donner la formule qui permet de calculer AM en fonction de AB, α et β

Tu dois donc avoir un résultat où figurent a, α, β

La réponse $AM=asinβsin⁡(180−α−β)AM=a\frac{sin\beta}{\sin(180-\alpha-\beta)}$

estbonne

Si tu connais les sinus des angles supplémentaires :

La réponse

$\fbox{AM=a\frac{sin\beta}{\sin(\alpha+\beta)}}$

est très bonne.

C'estLA réponse.

Ah oui exact, j'avais oublié, merci beaucoup, bonne journée

De rien !

A+