Etudier les variations et tracer la courbe représentative à l'aide de la fonction dérivée

Bonjour à tous , je bloque sur cette exercice:

Soit une fonction numérique f définie sur [-1;5] et sa fonction dérivée f' , dont la courbe représentative dans le repère (O,I,J) est tracée ci dessous.

la courbe est une parabole decroissante de -1 a 2 en passant par le point 1 puis croissante de 2 a 5 en passant par le point 3.

1)a. A l'aide du graphique déterminer le signe de f'(x) suivant les valeurs de x.
b. En déduire les variations sur [-1;5].

On veut tracer une représentation graphique C possible de la fonction f.
On sait que : f(0) = 1 , f(1)= 1/3 , f(2) = -1/3, f(3) = -1 et f(4) = -1/3
a. Placer dans le repère (O,I,J) les points de C d'abscisses 1,2,3 et 4
b. Tracer la tangente à C au point d'abscisse 0. Tracer de même les tangentes à C aux points d'abscisses 1;2;3 et 4
c. proposé un tracé de la courbe C.
On veut déterminer l'expression de f(x). On suppose que pour tout réel x :
f(x) = 1/3x^3 + ax² + bx + c.
Déterminer les valeurs de a,b,c donner l'expression de f(x).

4)Peut on trouver d'autres fonctions admettant f' pour solution dérivée ?

Ce que j'ai fait :
a) jai mis que de -1 a 1 c'est positif puis négatif de 1 a 3 et enfin négatif de 3 a 5
b) croissant , decroissant , croissant

2)Ici je bloque je pense qu'il y'a une erreur dans l'énoncé. ils disent f(0) = 1 et f(4) = -1/3 donc sa decroit alors que sur le graphique la dérivée est positive jusqu'à 1 c'est contradictoitre avec f(0) et f(1) .

Merci pour votre aide.

Bonjour,

**point 1 ? point 3 ?**cela ne veut rien dire...
Tout point a deux coordonnées.

Précise les deux coordonnées des points dont tu parles.

Si tu as un graphique, tu peux le donner (sans le texte)

Je regarde de plus près...

Pour le "point 1", tu as peut-être voulu écrire (1,0) ?
Pour le "point 3", tu as peut-être voulu écrire (3,0) ?

Si c'est ça, tes réponses pour la question 1) sont exactes.

Pour la 2), effectivement, l'affirmationf(0)=1 ne convient pas.
f étant croissante sur [-1,1], on ne peut pas avoir f(0)=1 et f(1)=1/3.

Si tu prends par exemple, f(0)=-1 au lieu de f(0)=1, la question 2) se fait bien.

Il y a peut-être eu une faute de frappe dans l'énoncé ...

Je viens de faire la 3) sans me servir de f(0) et effectivement, j'obtiens f(0)=-1

Alors, je te conseille d'utiliser f(0)=-1 dans cet exercice.

c'est d'accord , merci beaucoup . Il y' a une erreur dans l'énoncé.
je vous envoies ce que j'ai fait dans quelque minute.

En faite j'ai placer mes points mais je n'arrive pas à faire les tangentes. je sais que pour cela il faut calculer le coefficient directeur mais je ne sait pas comment mis prendre. Merci pour votre aide

Tu ne peux pas "calculer" le coeffficient directeur dans la question 2) ; tu as son signe.

Tu dois tracer des tangentes, en conséquence de la question 1).

Tu ne la pas donné ici, mais j'ai cru comprendre que tu as la courbe de f '

Alors, tu peux lire, sur la courbe de f ', les valeurs des coefficients directeurs des tangentes, qui sont les nombres dérivés.

Soit a le coefficient directeur de la tangente.

Au point (0,-1) : a=f'(0) a>0 tu as une tangente "montante"
Au point (1,1/3) : a=f'(1)=0 (extremum) tu as une tangente horizontale
Au point (2,-1/3) : a =f'(2) a< 0 tu as une tangente "descendante"
Au point (3,-1) : a=f'(3)=0 (extremum) tu as une tangente horizontale
Au point (4,-1/3) : a =f'(4) a> 0 tu as une tangente "montante"

ah d'accord merci , mais je pense que f(4) = 1/3 et non pas -1/3 comme le dit l'énoncé .

Pour "chercher l'erreur d'énoncé", j'ai fait la question 3) en utilisant les points abscisses 1 , 2, 3 .

Les valeurs trouvées pour a, b, c, correspondent à f(0)=-1 et effectivement à f(4)=1/3

Alors, prends f(4)=1/3.

J'espère que ce n'est pas tout le temps que tu as un énoncé avec 2 erreurs!

Remarque : Pour que tu puisses vérifier tes calculs de la 3), je te donnes l'expression de f(x) trouvée :

$\text{f(x)=\frac{1}{3}x^3-2x^2+3x-1$

Voici ce que j'ai fait avec f(4) = 1/3 :
[i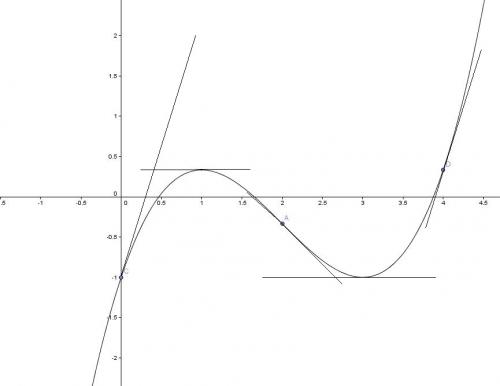 $fichier math$ mg][/img]

Oui , je pense que notre professeur va être indulgente sur cette exercice. Merci pour la 3) je pourrai verifier ce que j'ai fait

Ton graphique me semble très bien !

Bons calculs pour la 3)

Il y a trois inconnues a, b, c.
Il te faut donc trois équations.

Maintenant que les modifications sont prévues, prends les 3 points qui te semblent donner les calculs les plus simples ( surtout f(0)=-1 avec lequel tu arrives directement à c=-1 ).
Ensuite, vérifie que l'expression trouvée pour f(x) convient aux deux points non utilisés.

Merci , je bloque sur le systéme : 1² + 2a fois 1 +b = 0
3² +2a fois 3 + b = 0
merci pour votre aide.

Simplifie chaque équation écrite

$\left{1+2a+b=0\9+6a+b=0\right$

Par exemple, tu peux résoudre par substitution

Avec la 1ère équation : b=-1-2a

En substituant das la seconde : 9+6a-1-2a=0 en résolvant a=-2

Tu remplaces a par -2 dans une des équations ( n'importe laquelle) est tu trouves b=3

ah d'accord merci moi j'avais inversé un signe ce qui m'a donné tout faux.

Tu as donc maintenant l'expression de f(x).

Piste pour la 4) : pense que la dérivée d'une fonction constante vaut 0