Fonction Aire d'un triangle isocèle
-
YYoupiYoup dernière édition par
Bonjour,
Je dois répondre à une question qui pose pproblème, la voici :Soit ABC une triangle isocèle en A inscrit dans le cercle c, H le milieu de [BC] et x= AH (0<x<2R).
Montrer que l'aire S du triangle ABC vérifie :
S^2=x^3Voilà j'ai déjà fait plusieurs calculs mais à chaque fois je tombe sur des choses compliqué et jamais au résultat rechercher:
[img=http://www.mathforu.com/transfertfichier/fichiers/2904-fichier-math.jpeg]fichier math[/img]
[img=http://www.mathforu.com/transfertfichier/fichiers/2906-fichier-math.jpeg]fichier math[/img]
Merci d'avance
-
mtschoon dernière édition par

Bonjour,
Sauf si j'ai mal lu l'énoncé, ce que tu cherches à prouver (S²=x3=x^3=x3) est inexact.
Pour S tu dois obtenir une expression en foncrion de x et R
Par contre, tes calculs sont à revoir .
Tu idée est juste mais en développant BH il y a un double produit qui vaut 2Rx et tu as pris 2R
De plus, ensuite, la racine carré d'une différence n'est pas la différence des racines carrées.
Sauf erreur, tu dois trouver :
$\text{bh=\sqrt{2rx-x^2}$
$\text{s=bh\times ah=x\sqrt{2rx-x^2}$
Tu peux évidemment transformer cette expression ( pour (0 < x < 2R)
$\text{s=\sqrt{x^2}\sqrt{2rx-x^2}=\sqrt{x^2(2rx-x^2)}=\sqrt{2rx^3-x^4}$
$\text{s^2=2rx^3-x^4$
-
YYoupiYoup dernière édition par
Oh je suis vraiment désolée il faut vérifier que S^2=X^3(2R-x)
D'accord je vais revoir mes calculs
-
mtschoon dernière édition par

Cette fois, c'est bien ça !
Tu mets x3x^3x3 en facteur dans ma dernière réponse ce qui te donne effectivement
$\text{s^2=x^3(2r-x)$
Tu n'a plus qu'à revoir tes petites fautes de calcul pour y arriver.
-
YYoupiYoup dernière édition par
Merci beaucoup, cela fonctionne !
En revanche après il nous demande d'étudier la variations de la fonction x->x^3(2R-x) sur ]0;2R[ et d'en déduire que, parmi les triangles isocèles inscrits dans c, les triangles equilateraux sont d'aire maximale.
J'ai réussi à trouver quelque-chose mais il me semble y avoir une erreur, pouvez-vous vérifier s'il vous plaît ?
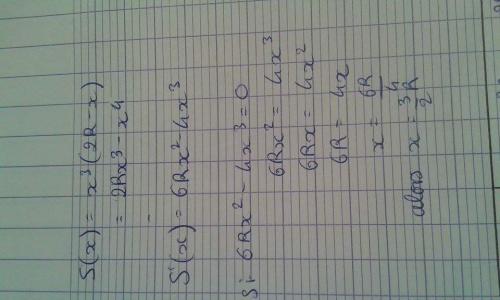
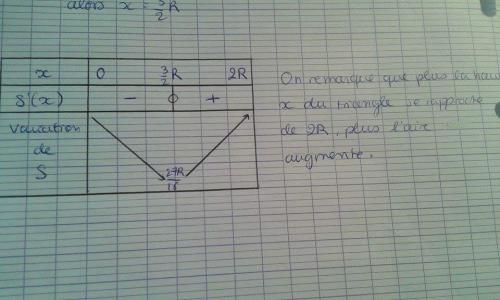
-
mtschoon dernière édition par

Fait attention aux notations.
Ce n'est pas S dont il s'agit, mais S²
Tu peux poser f(x)=S²(x) si ça t'arrange
Oui pour la dérivée mais tu as fais une erreur pour le signe de f' d'où pour le sens de variation de f
$\text{f'(x)=2x^2(3r-2x)$
Vu que 2R² >0 , f'(x) est du signe de 3R-2x
3R-2x > 0 <=> -2x > -3R <=> 2x < 3R <=> x < 3R/2
3R-2x < 0 <=> -2x < -3R <=> 2x <>3R <=> x > 3R/2Tu obtiens donc un maximum au lieu d'un minimum.
-
YYoupiYoup dernière édition par
D'accord merci beaucoup !
-
mtschoon dernière édition par

De rien, mais tu n'as pas tout-à-fait fini ton exercice !
Pour x=3R/2, tu viens de prouver que S² est maximale donc que S est maximale.
Reste à prouver que dans ce cas ABC est équilatéral, c'est à dire que AB=AC=BC(Tu dois trouver, après calculs que AB=AC=BC =√3 R)
Bons calculs.
-
YYoupiYoup dernière édition par
J'avais trouvé que l'aire d'un triangle isocèle = (√3/4)*L^2
Et donc A'=(√3/2)*L
A^2=3/2 *L soit x
Par conséquent l'aire maximale correspond à l'aire d'un triangle équilatéral.En prenant compte de votre remarque, j'ai essayé trouver votre résultat mais je n'arrive à rien. Est ce que je dois utiliser Pythagore ?
-
mtschoon dernière édition par

En remplaçant x par 3R/2, tu peux calculer BH qui vaudra √3R/2 d'où BC=√3R
Avec le théorème de Pythagore AB²=AH²+BH²=...= 3R² d'où AB=√3R
Tu trouves ainsi la conclusion, exclusivement dans l'esprit de l'exercice.
-
YYoupiYoup dernière édition par
Oui en effet, merci
-
mtschoon dernière édition par

De rien !
A+