Casserole Fonction

Bonjour ! J'ai un problème à résoudre, en voici l'énoncé :

Pour fabriquer une casserole d'un volume de 2 litres, une entreprise veut minimiser le coût en utilisant le moins de métal possible...

Comment doit-elle choisir le rayon et la hauteur de la casserole afin de réaliser cet objectif ?***(on ne tient pas compte ni de l'épaisseur du métal ni du manche!)*

~

Volume d'un cylindre = hπr²

Nous voulons un Volume de 2 litres.

Je complète mon expression :

2 L = hπr²

Ensuite, je suggère utiliser quelque chose que j'ai déjà appris en classe : l'aire et l'étude de fonctions. J'exprime l'aire en fonction de la casserole :

Aire cerlce = πr²
Aire surface latérale = 2πrh

Aire totale de la casselore = πr²+2πrh

Ensuite, je propose d'exprimer h grâce au volume :

v = πr²h ⇔ h = 2/π*r²

Est-bon pour le moment ?
Puis-je continuer en étudiant les variations de l'aire ?

merci !

Bonjour,

Tes débuts me semblent bons

En exprimant l'aire A en fonction de r, tu dois trouver après simplificaion :

$\text{a=\pi r^2+\frac{4}{r}$

Soit
$\text{f(r)=\pi r^2+\frac{4}{r}$

Tu étudies cette fonction f en fonction de r ( pour r > 0)

Aire totale de la casselore = πr²+2πrh

Comme h = 2/π*r² je remplace dans l'expression ; cela me donne :

A = πr²+ 2πr*(2/π*r²)

Je simplifie :

A = πr²+ 4/r

Nous obtenons une fonction polynôme du second degré que nous allons appeler f(r) :

f(r) = πr²+4/r+0

Pour le moment est-ce juste ?

Je n'ai pas bien lu la fin de l'expression f(r) que tu as écrit "+0" ?

f(r) = πr²+4/r pourr > 0

Attention : ce n'est pas une fonction polynôme du second degré à cause de 4/r
Si tu veux indiqué la nature de cette fonction (je ne pense pas que ce soit demandé), tu peux dire que c'est une fonction rationnelle.

D'accord, merci beaucoup.

f(r) = πr²+4/r

revient à écrire

f(x) = πx² + 4/x

avec

f'(x) = 2πx + 4/1
f'(x) = 2πx + 4

Etudions les variations de la fonction dérivée pour r > 0.

puis-je continuer ?

D'accord pour f(x) (avec x > 0) mais la dérivée est fausse.

La dérivée de 4/x n'est pas 4/1

Regarde ton cours.

$4x=4(1x)\frac{4}{x}=4(\frac{1}{x})$

Tu peux prendre la dérivée d'un quotient, mais je suppose que tu as la dérivée de 1/x, ce qui sera beaucoup plus rapide.

En regardant mon cours :

f'(x)= 2πx + 4*(-1/x²)
f'(x) = 2πx - 4/x2

?

C'est bon.

Tu peux réduire au même dénominateur et écrire :

$f′(x)=2πx3−4x2f'(x)=\frac{2\pi x^3-4}{x^2}$

Tu travailles sur ]0,+∞[ , x² > 0

Le signe de f'(x) est le signe de 2∏ $x^3$ -4

Trouvons la valeur qui annule la dérivée sur l'intervalle [0;+∞[ ;

x³ = 4/2π

Je bloque sur cette expression, je n'arrive pas à transférer le cube, je ne l'ai jamais fait.

Tu peux déjà simplifier par 2

$\leftrightarrow x^3=\frac{2}{\pi}$

Pour obtenir x, il faut prendre la "racine cubique".

J'ignorais que cela se faisait en Première...

Tu peux écrire

$x=2π3x=\sqrt[3]{\frac{2}{\pi}}$

ou bien

$x=(2π)13x=(\frac{2}{\pi})^{\frac{1}{3}}$

Sinon, à la calculette,x ≈ 0.86

Il s'agit de décimètres vu que le volume utilisé est exprimé en litres c'est à dire en $dm^3$

Je te mets un lien pour consulter la définition du terme "racine cubique" et la recherche pour les nombres réels

http://fr.wikipedia.org/wiki/Racine_cubique

Merci beaucoup pour le lien !

Je viens de consulter ma calculatrice effectivement, j'ai une touche spéciale où je peux taper l'expression : $2π3\sqrt[3]{\frac{2}{\pi}}$ !

Après peut-être il y a-t-il d'autres méthodes afin de résoudre le problème mais étant donné que nous sortons tout juste d'un chapitre sur les études de fonctions il me paraît plus logique d'utiliser cette méthode !

Dressons désormais le tableau de variation :

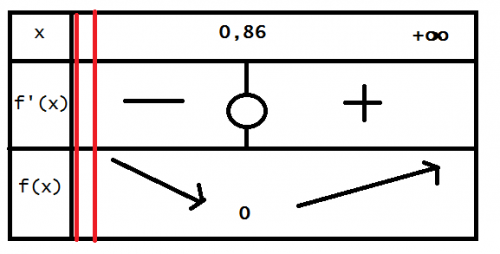
$fichier math$

(normalement à la place du "0.86" il y a l'expression " $(2π)13(\frac{2}{\pi})^{\frac{1}{3}}$ " , cependant je ne pouvais pas la taper sur paint !

J'en déduis que l'aire pour laquelle le rayon est minimale est pour x ≈ 0.86 dm

Maintenant que j'ai r, je peux remplacer r dans l'expression afin de trouver la hauteur :

h = 2/πr²

h = 2/π*[ $(2π)13(\frac{2}{\pi})^{\frac{1}{3}}$ ]²

h ≈ 0.86 dm = 8.6 cm ?

c'est bon pour r ≈ 8.6 cm et h ≈ 8.6 cm

Mais, dans ton tableau de variation, pour x ≈ 0.86, f(0.86) ne vaut pas 0

Effectivement, sur ma calculatrice je trouve f(0.86) ≈ 6.97

oui, c'est bien 6.97 dm², qui représente l'aire minimale de métal à utiliser pour faire la casserole .

J'ai une dernière question : on dit bien que la fonction f(x) est une fonction rationelle définie sur [0;+∞[ et donc dérivale sur [0;+∞[ ?

$f(x)=πx2+4x=πx3+4xf(x)=\pi x^2+\frac{4}{x}=\frac{\pi x^3+4}{x}$

f est le quotient de 2 fonctions polynômes : c'est une fonction rationnelle.

Condition d'existence et de dérivabilité pour toute fonction rationnelle : dénominateur non nul

Ici, f est définieET dérivable sur R*, donc en particulier sur ]0,+∞[

Fais attention au crochet : f n'est pas définie pour x=0 .
Dans ton exercice, il s'agit de ]0,+∞[ et non de [0,+∞[

*Remarque :

De façon générale, il ne faut pas dire f est définie DONC dérivable, car ce n'est pas une propriété applicable à tout type de fonction.

Toute fonction définie sur un ensemble D n'est pas forcément dérivable sur D.

Par exemple, la fonction "valeur absolue" (x->|x|) est définie sur R mais elle n'est pas dérivable au point d'abscisse 0 . Elle est dérivable seulement sur R**