Image directe et réciproque

[am9511]

Bonjour,

Je n'arrive pas à faire l'exercice merci de bien vouloir m'aider.

Exercice :

Soit A et B les ensembles définis en extension par : A={a,b,c} B={0,1,2,3}

on considère la fonction A->B définie par ses valeurs ci-dessous :
f(a)=0 f(b)=1 f(c)=2

1- Quel est l’image réciproque par f de {1,2} ?

Je ne sais pas comment faire

quelle est l’image réciproque par f de B ?
c’est {0,1}

2- Quelle est l’image directe par f de A ? c’est 0

3- Donner deux sous-ensemble de B dont l’image réciproque par f est l’ensemble vide. Y en a-t-il d’autres ? {d,e} oui une infinité

4- f est-elle injective ? oui
f est-elle surjective ? non

[Noemi]

Bonsoir am9511,

Comment est définie la fonction ?

[am9511]

désolé j'avais oublié : f(a)=0 f(b)=1 f(c)=2

[Noemi]

Quelle est l'image par f de {b,c} ?

[am9511]

{1,2} ?

[mtschoon]

Bonjour,

Visiblement, Noemi n' a pas pu passer encore pour te répondre.

Je regarde.

Oui, l'image de {b,c} est bien {1,2}

Tu peux en déduire que l’image réciproque par f de {1,2} est {b,c}

Si ce n'est pas déjà fait, je te conseille un graphique pour t'éclairer.

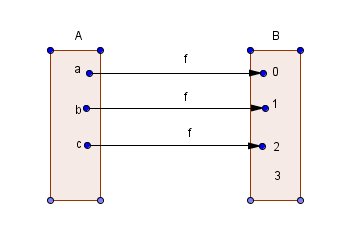
A part tes réponses à la 4) qui sont exactes, tes autres réponses sont à revoir.

Pour trouver l'image réciproque par f de B, cherche les antécédents de 0,1,2,3

Pour trouver l'image directe par f de A, cherche les images de a,b,c

B admet 16 sous ensembles ( $2^4$=16)
Passe en revue ces 16 sous-ensembles.
Tu en trouveras deux dont l'image réciproque par f est ∅ (il s'agit de ∅ et de {3} )

Reposte si besoin.