Dérivation Méthode de Newton ( méthode des tangentes )

Alors bonjour ! En fait voilà, durant mon examen, j'aurai un exercice concernant la méthode de Newton

exemple :

13x² + 4x +9 et je dois trouver les zéros en utilisant la méthode de Newton à 0.001 près si je ne me trompe pas

Et j'aimerai bien que vous m'expliquiez en quoi cette méthode consiste et si vous pouviez me donner un ou deux exercices pour que je m'exerce s'il vous plait, merci infiniment !

Bonjour,

Tu peux peut-être regarder ici :

http://villemin.gerard.free.fr/Calcul/Newton.htm

Consulte jusqu'à la fin de l'article : il y a la formule et un exemple traîté.

Alors merci beaucoup pour ce lien, mais malheureusement je n'ai pas très bien compris dans mon cours à moi c'est expliquer vite vite mais le truc c'est que je n'arrive pas à comprendre les étapes. Dans mon cours, on a utiliser delta et on a prit un zéros entre les 2 solutions trouver de delta et après BOOM je suis perdu !

Désolée, mais je ne peux vraiment pas t'aider pour ton cours ...

Une remarque :dans ton exemple, tu n'as pas dû donner la bonne expression car il n'y a pas de zéros (discriminant négatif)

Aaaaah dommage ... Il serait possible que je vous montre l'exemple que j'ai en cours ?

Comme je te l'ai indiqué,13x² + 4x +9 n'a pas de zéros ( il te suffit de calculer le discriminant pour le constater ) et utiliser la méthode de Newton pour un polynôme du second degré n'a guère d'intérêt vu que les formules usuelles permettent d'avoir les valeurs exactes des zéros.

Tu peux mettre l'exemple de ton cours bien sûr, mais il faut qu'il soit assez clair sinon il ne sera pas exploitable...

Oui j'ai donné un faux exemple c'est vrai. Bon, alors nous dans notre cours on a eu :

f(x) = 2x³ - 6x² + 3x - 4

On dérive

f'(x) = 6x² - 12x +3 = 3(2x² -4x + 1)

Zéros

x = 2± √2 /2 = 1,7 et 0,3

Tableau de signe

x	0,3 1,7
f'	+ 0 - 0 +

On dérive une seconde fois

f''(x) = 12x - 12 ( déjà ici je n'ai pas compris quelle équation nous dérivons

x	1
f''(x)	- 0 +

Tableau de variation

X	-∞ 0,3 1 1,7 +∞
F'	+ 0 - 0 +

F''	- 0 +

|

F | + max - PI - min +
-3,5 -5 -6,4

( PS : PI signifie point d'inflection et les " + et - " de la dernière ligne sont des fleches : + = flèche positif et - = flèche négatif )

( à partir d'ici, je ne comprends presque rien )
⇒ f admet une racine et cette racine est > 1,7

⇒ f(2) = -6 < 0
⇒ f(3) = 5 > 0

⇔ C ∈ ] 2 ; 3 [

On part du point d'abscisse 3

Tangente ≡ y - f(x) = f'(x) . (x-3)
≡ y-5 = 21(x - 3)

Tangente ∩ Ox : y = 0 ⇒ x1 = -5/21 +3 = 2,76
= | 27,6 - 3 | = 0,24 > 0,01

On répète le procédé à partir de x1. Il faut arrondir x1 correctement

f(x) = 2x³ -6x² + 3x -4

f'(x) = 6x² -12x +3

x1 = 2.76 soit x1 = 2,77

Tangente ≡ y - f(2,77) = f'(2,77). (x-2,77)
y - 0,78 = 15,79 ( x-2,77)

Tangente ∩ Ox : x2 = -0,78 / 15,79 + 2,77 = 2,72

| x2 - x1 | = | 2,72 - 2,77 | = 0,05 > 0,01 (⇒ On a pas atteint l'ordre de grandeur )

On arrondi par excès :

x2 = 2,73

Tangente ≡ y - f(2,73) = f'( 2,73).(x-2,73)
= y - 0,16 = 14,95 ( x-2,73)

Tangente ∩ Ox : x3 = 0,16/14,95 +2,73 = 2,71

| x3 - x2 | = | 2,71 - 2,73 | = 0,02 > 0,01

On arrondi par excès :

x3 = 2,72

Tangente ≡ y - f(2,72) = f'(2,72) . (x - 2,72)
= y - 0,01 = 14,75 (x - 2,72)

Tangente ∩ Ox : x4 = -0,01/14,75 + 2,72 = 2,719

| x4 - x3 | = | 2,719 - 2,72 | = 0,009 < 0,01

⇒ 2, 719... est une racine de f à 0,01 près

Voilà ! Merci encore de consacrer votre temps à nous aider et j'espère avoir été le plus clair possible, bonne journée !

Désolé pour les tableaux de signes et de variation, j'essaye de rajouter des espaces mais ça ne change rien

Bonjour,

Je regarde un peu.

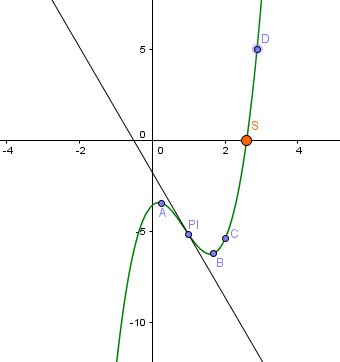
$fichier math$

Le début est l’étude de la fonction f (correspondant à la courbe tracée)
Le maximum relatif correspond au point A (0.3 ; -3.5)* (valeurs approchées)*
Le minimum relatif correspond au point B (1.7 ; -6.4) (valeurs approchées)

La dérivée seconde de f est la dérivée de f ’ ; elle se note f’’

f’(x)=6x²-12x+3 donc f ‘’(x)=12x-12

Cette dérivée seconde sert à chercher les points d’inflexion éventuels et la concavité de la courbe

Point PI : f’’(x)=0 <=> x=1 : Point d’inflexion.
La tangente en ce point « traverse la courbe »

f’’(x)<0 <=> x<1
Les tangentes en ces points sont au dessus de la courbe.
La courbe a sa concavité tournée vers « le bas »

f’’(x)>0 <=> x>1
Les tangentes en ces points sont en dessous de la courbe.
La courbe a sa concavité tournée vers « le haut »

Le zéro de la fonction est la solution de l’équation f(x)=0
Il correspond au point S (intersection de la courbe avec l’axe des abscisses). :
C’est l’abscisse de S, notée $x_S$ .Le but est de trouver des valeurs approchées de $x_S$ .

Vu le tableau de variation ( et la courbe), pour x < 1.7, f(x) < 0 donc l’équation f(x)=0 est impossible sur ]-∞ , 1.7]

Donc on va travailler sur ]1.7 ; +∞[

Pour préciser un intervalle où est située $x_S$ , f(2) et f(3) ont été calculées.

f(2)= -6 point C
f(3)= 5 point D
S est entre C et D
2 < $x_S$ < 3

Pour la méthode de Newton, on peut, par exemple, commencer à $x_0$ =3 (valeur choisie dans l'exercice)

Vois ce début de près.
Lorsque tu auras bien compris, j’essayerais de t’expliquer la méthode avec les tangentes successives (de Newton) pour trouver une valeur approchée de $x_S$ (fin de ton exercice)

Idée générale de la méthode des tangentes dans ton exercice.

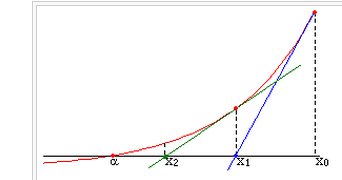
$fichier math$

α est $x_S$ dans le premier graphique

Je te conseille de tracer les tangentes sur ton graphique pour mieux comprendre.

On part de $x_0$ =3 point D de la courbe.
On cherche l’équation de la tangente (T1) à la courbe au point D
On cherche l’abscisse $x_1$ du point d’intersection de (T1) avec l’axe des abscisses

On recommence avec le point de la courbe d’abscisse $x_1$
On cherche l’équation de la tangente (T2) à la courbe au point de la courbe d’abscisse $x_1$
On cherche l’abscisse $x_2$ du point d’intersection de (T2) avec l’axe des abscisses

On recommence avec le point de la courbe d’abscisse $x_2$
On cherche l’équation de la tangente (T3) à la courbe au point de la courbe d’abscisse $x_2$
On cherche l’abscisse x3 du point d’intersection de (T3) avec l’axe des abscisses

Etc

à chaque étape on calcule | $x$ _{n+1} $x_n$ |

On s’arrête dès que | $x$ _{n+1} $x_n$ |<0.01 (ordre de grandeur)

Ici, on trouve | $x$ _4 $x_3$ | < 0.01

La valeur $x_4$ convient.

Bon courage pour tes révisions.

Bonjour ! En faite je ne comprends pas comment on trouve 2 comme descriminant alors que moi je trouve 8 et aussi, comment, dans le tableau de variation, nous trouvons que le maximum est en -3,5 , que le point d'inflexion est en -5 et le minimum est a -6,4 , merci beaucoup

f'(x)=3(2x²-4x+1)

Pour trouver les zéros, on peut bien sûr utiliser 6x²-12x+3 et simplifier les résultats trouvés(tu obtiendras les résultats donnés)

Vu la factorisation par 3, on peut utiliser seulement2x²-4x+1 (pour les zéros et pour le signe sans aucun changement vu que 3 est positif)
f'(x)=0 <=> 2x²-4x+1=0
f'(x)<0 <=> 2x²-4x+1<0
f'(x)>0 <=> 2x²-4x+1>0

Avec 2x²-4x+1 :

Δ=8
Tu peux calculer les zéros et après simplification, tu obtiendras les résultats donnés.

Vu que b est pair, tu peux calculer le discriminant réduit Δ', si tu connais
b=-4 donc b'=-4/2=-2
Δ'=b'²-ac=2

$x1=−b′−δ′a=2−22x_1=\frac{-b'-\sqrt{\delta'}}{a}=\frac{2-\sqrt 2}{2}$
$x2=−b′+δ′a=2+22x_2=\frac{-b'+\sqrt{\delta'}}{a}=\frac{2+\sqrt 2}{2}$

Pour les extrema (le maximum et le minimum) , ton cours utilise des valeurs approchées.

En principe, on met les valeurs exactes dans un tableau de variation, mais dans ton cours, il semble que ça soit les valeurs approchées qui soient mises, pour faire plus simple.

A la calculette :
$\frac{2-\sqrt 2}{2}\app 0.30 \ \frac{2+\sqrt 2}{2}\app 1.70$

Pour trouver les ordonnées associées, tu utilises l'expression de f(x) et tu remplaces x par les valeurs utiles 0.30 et 1.70 (à la calculette, c'est facile)

$f(0.30) \app -3.5 \ f(1.70) \app -6.4$

Pour le point d'inflexion (je t'ai déjà donné des indications)
f"(x)=0 <=> 12x-12=0 <=> x=1

Pour trouver l'ordonnée associée, tu utilises l'expression de f(x) et tu remplaces x par 1

$f (1) = - 5$

Ah d'accord je comprends mieux !! Merci beaucoup je vais poursuivre de suite alors, merci beaucoup

Bonjour ! Bah voilà j'ai trouver le même résultat, mais auriez-vous un exercice que je pourrai faire pour m'entraîner s'il vous plait ?

Si tu parles de t'entraîner pour les études de fonctions du 3ème degré, tu peux éventuellement consulter ici :

http://passeport.univ-lille1.fr/site/Math-va/cdmath/e1057/e1057et3.htm

Oui merci et pour m'entraîner à faire Newton ?

Pour la méthode de Newton, je ne peux pas te proposer d'exercice corrigé car ton cours est seulement une introduction à la méthode.La formule usuelle (que je t'ai indiqué en lien dans ma première réponse) n'en fait pas partie alors que tous les exercices corrigés l'utilisent.

Voici un lien où il y a la fonction et les premières valeurs de x1, x2,...
Pour t'entraîner, tu peux calculer x1, x2,...comme dans ton cours et t'assurer que tu trouves pareil

https://fr.wikipedia.org/wiki/Méthode_de_Newton#Exemple