Fonctions-conjecture c'est le Vide

la question 1 me demande de faire la conjecture mais en coure je viens jute de relire touts mes cours je n'ai jamais vue ça alors j'ai mis les deux équation sous forme de graphe et j'obtiens deux paraboles.
la question 2 ils me demande de démontrer la conjecture 1 mais là c'est le vide je ne comprend pas

en vous remerciant par avance

Merci d'écrire l'énoncé à la main.

BONJOUR !

Ici, les énoncés doivent être écrits à la main (pas de texte scanné)

Merci d'écrire l'énoncé à la main.

ah ok mais je l'ai fais une fois et Noémi ne m'a rien dit
alors
Soient f et g deux fonction définies se $mathbb{R}$ par f(x)=x² et g(x)=x-2x+1

A l'aide de la calculatrice, conjecturer la position relatif des courbes Cf et Cg sur $mathbb{R}$
Démontrer la conjecture de la question 1

la question 1:
me demande de faire la conjecture mais en coure je viens jute de relire touts mes cours je n'ai jamais vue ça alors j'ai mis les deux équation sous forme de graphe et j'obtiens deux paraboles.
la question 2:
ils me demande de démontrer la conjecture 1 mais là c'est le vide je ne comprend pas

en vous remerciant par avance

Bonjour,

La forme de g(x) est bizarre : x-2x+1 ??
Cela se réduit.
Tu devrais pour commencer vérifier ton énoncé.

à désoler pour
g(x)=x²-2x+1

Il s'agit donc de deux paraboles.
Que remarques-tu sur ces courbes ? Se coupent-elles ? L'une est-elle au-dessus de l'autre ?
Ce que tu peux observer sur ton dessin te permet de dire ce que tu en penses : c'est cela "conjecturer".

j'ai remarqué que les deux paraboles se coupent en un même point sur l'axe des abscisses

Ce point n'est pas situé sur l'axe des abscisses.
Fais un dessin précis.
Donne les coordonnées du point commun.

après avoir retracé mes paraboles deux fois car j'ai fais des erreur de calcule j'ai trouvé le point où les deux paraboles se coupent les différentes cordonnées sont (0.5;0.25)

Attention à l'expression : il n'y a pas "différentes" coordonnées : (0.5 ; 0.25) est le couple des coordonnées du point.
A gauche de ce point, comment sont les deux courbes (laquelle est au-dessus de l’autre ?), et à droite ?

à gauche f(x) est plus petite que g(x)
à droite g(x) est plus grand que f(x)
alors je suppose que c'est g(x) qui est au-dessus de f(x)

Citation
à gauche f(x) est plus petite que g(x)Oui.
Citation
à droite g(x) est plus grand que f(x)Non : c'est le contraire : observe mieux.
Trace les courbes avec des couleurs différentes. Comme on te demande les positions relatives de Cf et Cg, indique plutôt "dessus" ou "dessous".

ah oui vous avez raison en utilisant la fonction table de la calculatrice
f(x) est plus grand

Non.
Laisse maintenant ta calculatrice et observe le dessin.
Tu peux joindre ce dessin avec la fonction "ajoute une image" en bleu en bas de la fenêtre de saisie.

ah ok j'avais pas compris ce que vous vouliez vous voulez que je vous envoie mon dessin via le scan?
j’espère que ça sera lisible désoler d’avance

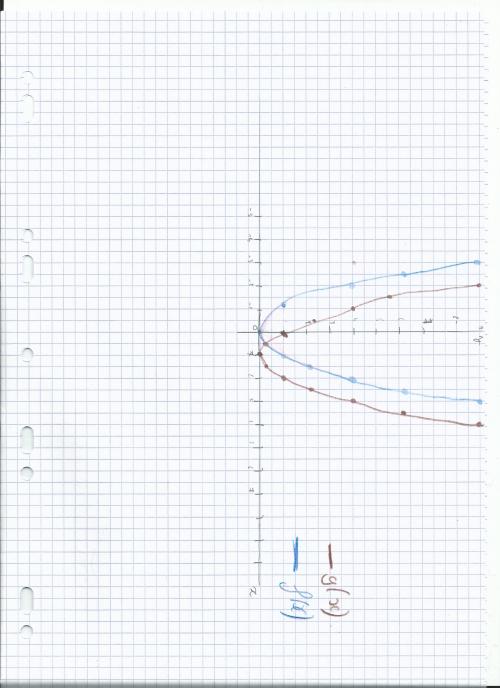$fichier math$ si ce n'es pas vraiment lisible

ah ok j'avais pas compris ce que vous vouliez vous voulez que je vous envoie mon dessin via le scan?
j’espère que ça sera lisible désoler d’avance

$fichier math$ si ce n'es pas vraiment lisible

Il faut le mettre dans l'autre sens : l'axe des abscisses horizontal, et l'axe des ordonnées vertical, sinon "dessus" ou "dessous" n'ont plus aucun sens.

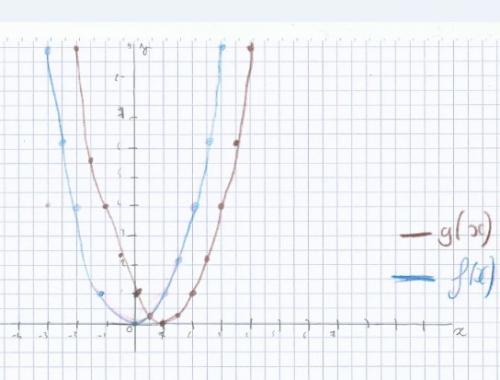$fichier math$ j'ai fais le graphique en paysage j'ai pas prévenu désoler

Il n'y a plus qu'à observer :
à gauche du point commun, Cf (bleue) est en dessous de Cg (noire)
à droite du point commun, Cf est au-dessus de Cg.
Fin de la première question.
Maintenant, tu dois démontrer cette conjecture en utilisant des inégalités sur f(x) et g(x).
Je te conseille de calculer f(x) - g(x) et d'étudier le signe de cette différence.

c'et à dire que je dois commencé par
=x²-x²-2x+1

je suis pas vraiment rassuré du résultat qui est -2x+1

En effet, il est faux.
Tu dois savoir que pour éviter ce genre d'erreur il faut placer des parenthèses :
f(x) - g(x) = x² - (x² - 2x +1) = ...

après réflexion je pense avoir trouvé la réponse qu iest
$2x^{3 }$ -3x²

C'est pire !
De plus je ne vois pas quelle sorte d'erreur tu as commise : aurais-tu multiplié au lieu de soustraire ? (même dans ce cas, ce serait faux).

Depuis le collège, tu devrais savoir "supprimer" des parenthèses.
a-(b-c+d) = a-b+c-d
Ici : x² - (x² - 2x +1) = ??

ok désolé si j'ai je n'ai pas répondu directement mais ma connexion Internet à sauter

je n'ai absolument pas pensé à supprimé les parenthèse car vu que j'ai vu une parenthèse et un nombre devant j'ai pensé a la développer (la distributivité)

mon raisonnement
=x²-x²+2x-1
=2x-1

je pence que le résultat est 2x-1

Citation
je n'ai absolument pas pensé à supprimé les parenthèse car vu que j'ai vu une parenthèse et un nombre devant j'ai pensé a la développer (la distributivité)
Même dans ce cas, le calcul aurait été faux.

La différence vaut bien 2x - 1
Maintenant il faut étudier son signe : facile, c'est du premier degré.

pour etudié le signe de cette fonction je vais faire un tableau de signe

x | -∞ -0.5 | 0 +∞ |
f(x) | - 0 | + |

Ton tableau n'est pas clair.
0 n'a rien à faire dans ce tableau.
En revanche, il y a une erreur : 2x-1 s'annule pour x = 0.5, pas -0.5.
Enfin, évite de donner à 2x-1 un nom déjà utilisé. Utilise, par exemple, d(x) puisqu'il s'agit de la différence f(x) - g(x).

Quand tu auras corrigé, utilise tes signes afin de comparer f(x) et g(x) pour en déduire la position relative des deux courbes.

je suis désolé si le tableau n’étais pas clair

c'est bon j'ai corrigé mais qu'es que tu veux dire par
"utilise tes signes afin de comparer f(x) et g(x) pour en déduire la position relative des deux courbes."

Je dois utilisé mon tableau de signe pour comparé f(x) et g(x) et comment je fais pour déduire la position relatif des deux courbes si c'est signe avec le tableau de signe

Pour x<0.5, f(x) - g(x) <0, donc f(x) < g(x), donc Cf est en dessous de Cg.
Fais de même pour l'autre intervalle.

c'est bon alors j'ai obtenu aussi que Cf est en dessous de Cg

Non. C'est contradictoire avec ton dessin.
Détaille.

Pour x<0, g(x) - f(x) <0.5, donc g(x)

Shadowtin

Citation
Pour x < 0, g(x) - f(x) < 0.5, donc g(x)Ce n'est pas cela du tout.
Je t'ai dit que 0 n'a aucune raison de figurer en première ligne du tableau : c'est 0.5 qui commande les deux intervalles : ]-∞;0.5[ et ]0.5;+∞[.
Dans le premier intervalle (si x < 0.5), f(x) - g(x) est négatif, donc f(x) < g(x), donc Cf est en dessous de Cg.
Fais la même chose pour l'autre intervalle, en détaillantcomme je viens de le faire.

]-∞;0.5[ tu l'a fais pour cette intervalle je dois donc faire pour cette intervalle ]0.5;+∞[.
donc dans le second intervalle x > 0.5 donc g(x) - f(x) est positifs
donc g(x) < f(x), donc Cg est en dessous de Cf

Non.
Observe tout de même ton tableau !
Pour x > 0.5, la différence f(x) - g(x) (toujours la même) est positive, donc f(x) > g(x), donc Cg est bien en dessous de Cf, mais ta conclusion (juste) n'était pas conforme à ton inégalité (fausse).
Reprends cet exercice à tête reposée et en réfléchissant. Il est absolument nécessaire que tu comprennes tout.

mon inégalité x>0.5 est fausse mais me résultat que j'ai donné est juste si
j'ai bien compris

Non : tu te places dans le second intervalle pour lequel x > 0.5.
C'est l'inégalité " g(x) - f(x) est positifs" qui est fausse (et donc la suivante).
C'est f(x) - g(x) qui est positif dans cet intervalle, et non pas g(x) - f(x).

ok
alors
x > 0.5 f(x) - g(x) est positif, donc f(x) < g(x), donc Cg est bien en dessous de Cf

f(x) - g(x) est positif, donc f(x) > g(x) et pas le contraire !
Je démissionne.
Bon courage tout de même.

bon bha merci
dessolé si je vous ai énervé mais après 10h de bouleau non stop c'est très fatigant de se concentrer.
Merci de m'avoir aidé pour cet exercice et de m'avoir redonné quelque base en Maths car c'est pas mon prof qui allais le faire cette année
sinon ton site Mathématiques à bâtons rompus est très sympa

Cordialement

Shadowtin_by_Quent