Réaliser l'étude complète d'une fonction avec racine carrée

Alors bonjour, pour mon examen, j'aurai à faire 1 des 6 études complète et j'aimerai bien que vous me montriez comment les faire s'il vous plaît parce que je m'en sors pas pour chaque point .. Merci ! Alors la fonction est :

F(x) =√x²-3x+2 ( la racine prend toute l'équation )

Alors les points à faire sont =>

le domaine de la fonction
la parité
le comportement aux bornes ( les limites et asymptotes )
( je ne comprends pas très bien les limites )
la dérivée première et ses zéros
la derivee seconde et ses zéros
les points particuliers ( minimum, maximum, point d'inflexion etc ) je ne comprends pas tres bien non plus
graphe de f ∩ avec l'axe oy
graphe de f ∩ avec l'axe ox
et le graphe

encore une fois, merci beaucoup pour l'aide que vous m'apportez !

Bonjour,

Il y a des questions auxquelles tu dois pouvoir répondre, je pense.

Commence par indiquer ce que tu as fait pour le domaine de définition et nous vérifierons.

Pour comprendre, tu peux consulter ici :

https://www.youtube.com/watch?v=GgpGSjvtj3E

Bonjour. J'ai trouver ] -∞ ; 1 ] U [ 2 ; + ∞[

Ensuite j'ai fait la parité de la fonction et j'en ai conclus qu'elle n'est ni paire ni impaire.

Je ne sais pas faire les comportements aux bornes ni les points particuliers donc je suis passer aux derivées.

dérivée première

F'(x) = 2x-3 / √x²-3x+2

Zéro de la dérivée : 2x-3 = 0 -> x = 3/2

dérivée seconde

F''(x) = 2

Et je ne sais pas aller plus loin

Ce que tu as fait est bon pour le domaine et la parité.

f'(x) et f"(x) sont à revoir.

Pour les limites en +∞ et -∞

$lim⁡x→±∞(x2−3x+2)=lim⁡x→±∞(x2)=+∞\lim_{x \to {\pm \infty}}(x^2-3x+2)=\lim_{x \to { \pm \infty}}(x^2)=+\infty$

Vu que $lim⁡x→+∞x=+∞\lim_{x \to +\infty}\sqrt x=+\infty$

Tu peux déduire que :

$lim⁡x→±∞(x2−3x+2=+∞\lim_{x \to {\pm \infty}}(\sqrt {x^2-3x+2}=+\infty$

Vu qu'aucune indication n'est donnée et que j'ignore le contenu de ton cours, merci de dire ce que tu sais sur la recherche d'asymptotes.

Ah ces limites ... Vraiment dur franchement ! Bah recherche d'asymptotes oblique, horizontal et verticale mais je pense qu'il n'y a pas d'asymptotes horizontal déjà car la limite est en + ∞ non ?

Il y a deux asymptotes obliques mais j'ignore la méthode de ton cours pour les trouver....Indique la.

Lorsque l'équation de l'asymptote oblique n'est pas donnée dans l'énoncé, en principe on fait cela :

http://homeomath2.imingo.net/oblique.htm

Je vais chercher ça et je comprends pas pour la dérivée et je sais que pour les asymptote oblique, il faut d'abord chercher le "a" puis le "b", un truc comme ça quoi

Pour la dérivée f' :

formule usuelle

$(u)′=u′2u(\sqrt u)'=\frac{u'}{2\sqrt u}$

Pour f" (dérivée de f'), utilise la dérivée d'un quotient (formule usuelle)

$(uv)′=u′v−uv′v2(\frac{u}{v})'=\frac{u'v-uv'}{v^2}$

Pour trouver a et b d'une asymptote oblique, les formules sont marquées dans le lien que je t'ai donné dans ma réponse précédente.

J'espère que c'est indiqué dans ton cours, car vu la fonction que tu proposes, il n'y a pas d'autre solution...

Pour x tendant vers +∞, tu dois trouver a=1 et b=-3/2, d'où asymptote oblique d'équation $y=x−32y=x-\frac{3}{2}$

Pour x tendant vers -∞, tu dois trouver a=-1 et b=3/2, d'où asymptote oblique d'équation $y=−x+32y=-x+\frac{3}{2}$

Bons calculs !

Bonjour.

Pourriez-vous mettre les calcules pour arriver à -3/2 car moi je trouve -2/3 en faite et je voudrais savoir comment on peut savoir si on utilise (√f), ou (√x)' ? Merci beaucoup !

Lorsque x tend vers +∞

Tu as trouvé je suppose : $lim⁡x→+∞f(x)x=1\lim_{x\to +\infty}\frac{f(x)}{x}=1$

donc $a = 1$

Il faut chercher $lim⁡x→+∞[f(x)−ax]=lim⁡x→+∞[f(x)−x]\lim_{x\to +\infty}[f(x)-ax]=\lim_{x\to +\infty}[f(x)-x]$

$f(x)−x=x2−3x+2−xf(x)-x=\sqrt {x^2-3x+2}-x$

Forme indéterminée lorsque x tend vers +∞

On passe par la quantité conjuguée

$f(x)−x=(x2−3x+2−x)(x2−3x+2+x)x2−3x+2+x=x2−3x+2−x2x2−3x+2+x=−3x+2x2−3x+2+xf(x)-x=\frac{(\sqrt {x^2-3x+2}-x)(\sqrt{x^2-3x+2}+x)}{\sqrt{x^2-3x+2}+x}=\frac{x^2-3x+2-x^2}{\sqrt {x^2-3x+2}+x}=\frac{-3x+2}{\sqrt {x^2-3x+2}+x}$

En prenant la limite en +∞, tu dois trouver b=-3/2

J'ai oublié ta question sur les dérivées.

La dérivée de √x est un cas particulier de la dérivée de √f

$(f)′=f′2f(\sqrt f)'=\frac{f'}{2\sqrt f }$

pourf(x)=x, f'(x)=1 d'où

$(x)′=12x(\sqrt x)'=\frac{1}{2\sqrt x }$

Ah bon c'est décider , je ne comprends rien ! Je trouverai un moyen de comprendre, pouvez-vous m'expliquer les autres points à faire s'il vous plait ? Histoire que j'ai un modèle pour faire les autres merci !!

Indique clairement ce que tu ne comprends pas avant d'essayer d'aller plus loin car avancer sans comprendre ne me semble pas être une bonne méthode .

Les limites et asymptotes que je n'ai pas compris et pour le reste ( Gf∩ox/oy , points particuliers) c'est la méthode que je ne connais pas, je ne vois juste pas comment les faire

Pour les limites et asymptotes j'essaierai de détailler lorsque j'aurai plus de temps (mais je te conseille de revoir ton cours)

Pour la dérivée première et la dérivée seconde : je t'ai donné les formules . Revois tes calculs et donne tes nouvelles réponses pour vérification

Pour les zéros de la dérivée première, tu résousf'(x)=0
Pour les zéros de la dérivée seconde, tu résousf"(x)=0

Ensuite tu fais le tableau de variation ( méthode tout à fait usuelle, que tu as vu dans l'exercice sur "Newton")
Tu pourras en déduire ( comme dans l'exercice sur "Newton") les points particuliers.

Intersection de la courbe avec l'axe des ordonnées (x=0), tu calculesf(0).

Intersection de la courbe avec l'axe des abscisses (y=0), tu résousf(x)=0

Bonjour.

Pour la derivée première j'ai trouver 2x-3 / 2. √x²-3x+2 . Et j'ai trouver 3 comme zéros . Mais je pense que c'est faux, franchement je ne vois pas

Et pour Gf intersection ox j'ai trouver √2 et pour Gf intersection oy j'ai trouver ±√1

Je regarde tes dernières réponses.

La dérivée première este exacte mais faut aussi penser en plus à son domaine de définition.
$f′(x)=2x−32x2−3x+2f'(x)=\frac{2x-3}{2\sqrt {x^2-3x+2}}$

Le dénominateur de la dérivée devant être non nul (on ne peut pas diviser par 0), la condition de dérivabilité est x²-3x+2 > 0

Le domaine de définition de f' est Df'=]-∞,1[ U ]2,+∞[

La fonction f est définie sur ]-∞,1] U [2,+∞[ et dérivable sur ]-∞,1[ U ]2,+∞[

Le zéro que tu as trouvé pour f' est très bizarre...

f'(x)=0 <=> 2x-3=0 <=> x=3/2

Cette valeur ne convient pas car 3/2 ∉ Df'

f' n'a pas de zéro

Je te conseille de fairele tableau de variation de f vu qu'il s'agit d'une étude complète (c'est le coeur de toute étude de fonction)

En ce qui concerne les intersections avec les axes, tu as confondu axe des abscisses avec axe des ordonnées.

Intersection de la courbe avec l'axe des ordonnées (axe (Oy) d'équation x=0), tu calcules f(0) : f(0)=√2
L'intersection de la courbe avec l'axe(Oy) est donc le point A de coordonnées (0,√2)

Intersection de la courbe avec l'axe des abscisses (axe (Ox) d'équation y=0), tu résous f(x)=0
Je ne comprends pas ton résultat car l'équation x²-3x+2=0 a déjà été résolue
x²-3x+2=0 <=> x=1 ou x=2
L'intersection de la courbe avec l'axe(Ox) est composée de deux points : le point B de coordonnées (1,0) et le point C de coordonnées (2,0)

Revois tout cela tranquillement (aller vite ne sert à rien, prends le temps de bien faire le travail) et continue l'exercice.

Bon courage.

Oui je referais tout ça ce soir et essayerai de calculer f'' aussi

Bonjour.

Voilà j'essaye de faire la derivee seconde mais je me perds dans mes calcules, j'ai écrit que

: (2x-3)'.(2√x²-3x+2) - (2x-3).(2√x²-3x+2 / 4x²-3x+2

Ensuite j'ai dérivée 2x-3 mais après je derive (2√x²-3x+2) et ça fait des racines sur racines et je me perds, merci beaucoup pour votre aide !

$\ u'(x)=2 \ v(x)=2\sqrt{x^2-3x+2} \ v'(x)=2\times\frac{2x-3}{2sqrt{x^2-3x+2}}=\frac{2x-3}{\sqrt{x^2-3x+2}}$

Donc :

$f′′(x)=4x2−3x+2−(2x−3)22x2−3x+24(x2−3x+2)f''(x)=\frac{4\sqrt{x^2-3x+2}-\frac{(2x-3)^2}{\sqrt{2x^2-3x+2}}}{4(x^2-3x+2)}$

$f′′(x)=4(x2−3x+2)−(2x−3)2x2−3x+24(x2−3x+2)f''(x)=\frac {\frac{4(x^2-3x+2)-(2x-3)^2}{\sqrt{x^2-3x+2}}}{4(x^2-3x+2)}$

$f′′(x)=4(x2−3x+2)−(2x−3)24x2−3x+2(x2−3x+2)f''(x)=\frac{4(x^2-3x+2)-(2x-3)^2}{4\sqrt{x^2-3x+2}(x^2-3x+2)}$

Tu simplifies le numérateur et tu dois trouver :

$f′′(x)=−14x2−3x+2(x2−3x+2)f''(x)=\frac{-1}{4\sqrt{x^2-3x+2}(x^2-3x+2)}$

Bonjour.

J'ai trouver les mêmes calculs heureusement et j'ai dresser mon tableau de variation mais le problème c'est que quand je remplace, par exemple, -1 dans f'' pour avoir son y bah la calculatrice me dit que c'est impossible et de même pour f' est-ce normal ?

Je t'ai indiqué Df'

Je te suggère de déterminer aussi Df''

-1 fait partie des ensembles de définition donc f'(-1), f''(-1) existent.

Tu peux même faire les calculs à la main, car ils sont simples.

Si tu as besoin d'une vérification, indique ton tableau de variation.

Justement le truc c'est que quand je remplace -1 dans f'' donc :

F''(-1) = -1 / 4x√(-1)²-3x(-1) +2 x( (-1)²-3x(-1)+ 2 ça fait :

= -1 / 4x√6 x 7 alors ?

Et pour le tableau de variation j'ai mis :

X | -1 1 3/2 2

f(x) | ++ 0 ---- 0 + + +

f'(x) | -- ∅ ++

f''(x) | ---0 --------

Je ne vois pas de quoi tu parles en ce qui concerne f''(-1)

$f′′(−1)=−146×6=−1246f''(-1)=\frac{-1}{4\sqrt 6 \times 6}=\frac{-1}{24\sqrt 6}$

$f''(-1) \app -0.017$

D'ailleurs, à quoi te sert de calculer f"(-1) ?

Pour le tableau de variation, j'ignore tes habitudes, mais en principe on symbolise les variations de f par des flèches (c'est même le but).
Evidemment, je n'ai pas ton cours ! ! !

Dans la ligne des "x" , 3/2 n'est pas à marquer vu qu'il n'appartient pas à l'ensemble de définition.
Il n'y a rien entre 1 et 2 ( tu peux même hachurer toute cette zone, pour bien montrer qu'elle ne fait pas partie de l'ensemble de définition)

Je te joins un tableau de variation ( fait seulement à la main car les tableaux à faire en Latex ne sont pas faciles...)

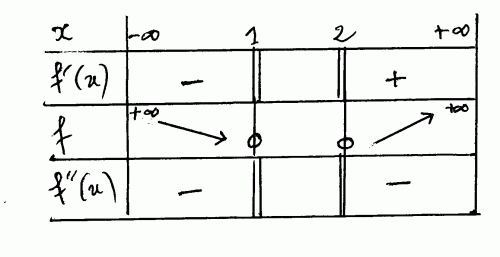
$fichier math$

Je te mets un lien à consulter éventuellement où il y a des exemples de tableaux de variation de fonctions

http://www.xm1math.net/premiere_es/prem_es_chap4_cours.pdf

Vu que pour f" on a trouver -1 , il faut bien qu'on calcule son y non ?

Et pour le tableau de variation, nous on fait d'abord avec des plus et moins ensuite on trace une ligne en dessous et on remplace ( par les flèches pour f' et par des concavités pour f" ) mais alors pour calculer les y des zéros et du point d'inflexion je fais comment ?

Tu as écrit
:
Citation
Vu que pour f" on a trouver -1 , il faut bien qu'on calcule son y non ?

Cela n'a pas de sens...

-1 ne correspond pas a une abscisse !

le numérateur de f''(x) est $- 1$
le dénominateurde f"(x) est $4\sqrt{x^2-3x+2)(x^2+3x+2} \$

J'espère que tu comprends que f''(x) est existe pour :
x ∈]-∞,1[ ∪]2,+∞[ ( revois l'explication donnée pour f')

Sur Df"=]-∞,1[ ∪]2,+∞[
le numérateur de f"(x) est négatif
le dénominateur de f"(x) est strictement positif, doncf"(x) < 0

f" n'a pas de zéro (pas de point d'inflexion)

Sur chacun des intervalles ]-∞,1[ et ]2,+∞[, vu que f"(x)<0, la courbe a sa concavité tournée "vers le bas"

Tu as aussi écrit :
Citation
calculer les y des zéros et du point d'inflexion je fais comment ?

"les y des zéros ???" . De quels zéros parles-tu ? Quels zéros as-tu trouvés ?

Je reste perplexe...

Oui je viens de comprendre! Vu que f' n'a pas de zéros, qu'il n'est pas compris dans notre domaine, ça sert à rien de le mettre dans le graphe c'est bien ça ?

Et des asymptotes verticales on en a pas ? Et pour la pente de l'asymptote verticale, on fait comment ?

Effectivement, f' et f" n'ont pas de zéro

Non, il n'y a pas d'asymptote verticale ( regarde la définition d'asymptote verticale dans ton cours)

Citation
La pente d'une asymptote verticale?

Je me demande ce que tu veux dire ...

Eventuellement, consulte ici

http://yallouz.arie.free.fr/terminale_cours/asymptotes/asymptotes.php

Ah désoler je voulais dire oblique * ^^'

Dur,dur...

Demain je tacherai de te donner une explication assez précise sur les asymptotes obliques ( vu que mon explication sur ce sujet n'a visiblement pas suffit...mais tu peux la revoir )

Je te mets le graphique ( courbe et asymptotes ) mais assure toi que tu sais le faire car c'est toi qui passe un examen, pas moi...

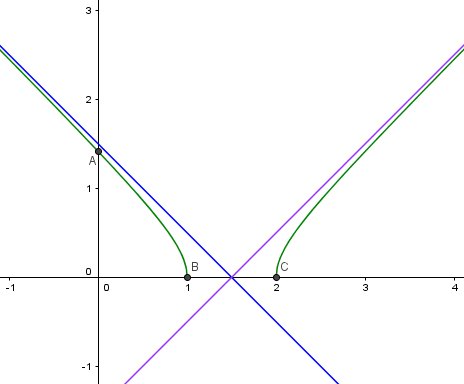
$fichier math$

Oui franchement c'est pas votre explication le problème c'est juste moi qui arrive pas à comprendre les chapitres sur les limites et asymptotes, le reste ça peut encore aller, vraiment merci pour votre aide, ah le temps passe et il m'en faut encore 5 , c'est vraiment dur pour moi ceux là !

Ah non j'ai refait le graphe a la perfection ! J'ai simplement remplacer x par une valeur dan les équations des asymptotes oblique ( y = -x + 3/2 et y= x-3/2 ) et j'ai eu le bon graphe , merci beaucoup

Je tente de te donner une explicationau voisinage de +∞

Si tu as une calculatrice graphique ( ce que j'ignore), je te conseille de commencer à représenter la courbe sur ta calculette pour te donner une idée.
Avec la fonction TABLE, tu peux avoir ainsi les valeurs de f(x) en donnant la valeur de x.
Par exemple, avec la fonction f définie par $f(x)=x2−3x+2f(x)=\sqrt{x^2-3x+2}$ , tu peux lire :
$f(100) \app 98.5 \ f(1000)\app 999.5$
Tu peux donc conjecturer que f(x) tend vers +∞ lorsque x tend vers +∞

Cela n'est pas à écrire dans un devoir bien sûr, c'est seulement pour avoir un aperçu.

Pour l'explication mathématique, précédemment, en ±∞, j'avais utiliser la propriété relative au terme de plus fort degré d'un polynôme *(lorsque x tend vers ±∞, la limite d'un polynôme est la limite de son terme de plus fort degré) *
Ainsi la limite de x²-3x+2 (en ±∞) est la limite de x².

Vu que tu n'as pas compris, je ne vais pas utiliser cette propriété (qui ne fait peut-être pas partie de ton cours)

Etude en +∞ ( tu fera seul l'étude en -∞, si tu le souhaites)

Bien sûr, je ne peux pas détailler toutes les explications...

f a une forme indéterminée du type "∞-∞"
Pour lever l'indétermination, on mets x² en facteur

$f(x)=\sqrt{x^2(1-\frac{3}{x}+\frac{2}{x^2})}=\sqrt{x^2}\sqrt{1-\frac{3}{x}+\frac{2}{x^2}$

On prend x positif ( pour des valeurs voisines de +∞) donc $sqrt{x^2}=x$

f(x) peux donc s'écrire dans ce cas :

$f(x)=x\sqrt{1-\frac{3}{x}+\frac{2}{x^2}$

Avec cette forme, la limite se trouve aisément.

1 est fixe
3/x tend vers 0
2/x² tend vers 0
donc 1-3/x+2/x² tend vers 1-0+0=1, donc la racine tend vers √1 =1

Un facteur (x) tend vers +∞ ; l'autre facteur tend vers 1 . Le produit tend donc vers +∞

$lim⁡x→+∞f(x)=+∞\lim_{x\to +\infty}f(x)=+\infty$

Essaie de comprendre ça.

Il y a possibilitéd'une asymptote oblique vu que f(x) tend vers +∞ lorsque x tend +∞

Parfois, dans les exercices, l'équation y=ax+b est donnée et il suffit alors de prouver que la limite def(x)-(ax+b) vaut 0 pour justifier que la droite d'équation y=ax+b est asymptote à la courbe.

Méthode usuelle lorsque l'énoncé ne précise rien

on cherche $lim⁡x→+∞f(x)x\lim_{x\to +\infty}\frac{f(x)}{x}$

En utilisant pour f(x) l'écriture trouvée précédemment :

$f(x)x=x1−3x+2x2x=1−3x+2x2\frac{f(x)}{x}=\frac{x\sqrt{1-\frac{3}{x}+\frac{2}{x^2}}}{x}=\sqrt{1-\frac{3}{x}+\frac{2}{x^2}}$

Lorsque x tend vers +∞, la limite de f(x)/x est donc 1 ( voir explication précedente)

Donc $\fbox{\lim_{x\to +\infty}\frac{f(x)}{x}=1=a}$

on cherche $lim⁡x→+∞[f(x)−ax]\lim_{x\to +\infty}[f(x)-ax]$

$f(x)−ax=f(x)−x=x2−3x+2−xf(x)-ax=f(x)-x=\sqrt{x^2-3x+2}-x$

forme indéterminée du type "∞-∞"

Il faut transformer cette écriture pour lever l'indétermination.

Comme je te l'ai déjà dit, on utilise la quantité conjuguée et une identité remarquable

Rappel : la quantité conjuguée de √A-B est √A+B

$a−b=(sqrta−b)(a+ba+b=a−b2a+b\sqrt a-b=\frac{(sqrt a -b)(\sqrt a+b}{\sqrt a+b}=\frac{a-b^2}{\sqrt a +b}$

En appliquant ce procédé à f(x)-x, on obtient :

$f(x)−x=−3x+2x2−3x+2+xf(x)-x=\frac{-3x+2}{\sqrt{x^2-3x+2}+x}$

(j'ai fait ce calcul dans une des réponses précédentes)

D'où

$f(x)−x=−3x+2x1−3x+2x2+xf(x)-x=\frac{-3x+2}{x\sqrt{1-\frac{3}{x}+\frac{2}{x^2}}+x}$

On met x en facteur au numérateur et au dénominateur et on simplifie.

$f(x)−x=x(−3+2x)x(1−3x+2x2+1)=−3+2x1−3x+2x2+1f(x)-x=\frac{x(-3+\frac{2}{x})}{x(\sqrt{1-\frac{3}{x}+\frac{2}{x^2}}+1)}=\frac{-3+\frac{2}{x}}{\sqrt{1-\frac{3}{x}+\frac{2}{x^2}}+1}$

Lorsque x tend vers +∞, 2/x, -3/x, 2/x² tendent vers 0

Il reste -3/(√1+1)=-3/1+1=-3/2

Donc $b = - 3 / 2$

$\fbox{\lim_{x\to +\infty}[f(x)-x]=\frac{-3}{2}=b}$

ASYMPTOTE d'équation :

$\fbox{y=x-\frac{3}{2}}$

J'ai pris le temps de te détailler car en période de vacances le forum est calme sinon, je n'aurais pas pu le faire...

J'espère que tu comprendras tout cela.