fonction avec valeur absolue et racine carrée
-
NNatsuDragneel dernière édition par
Bonjour, désolé de poster un autre exercice alors que le premier n'est pas fait mais le temps passe et j'ai encore tellement à faire et comme je vais pas me connecter souvent, je trouve mieux de poster à l'avance. Après, c'est comme vous voulez bien sûr ! La fonction est :
F(x) = √|x(x-1) |Alors les points à faire sont =>
- le domaine de la fonction
- la parité
- le comportement aux bornes ( les limites et asymptotes )
( je ne comprends pas très bien les limites )
) - la dérivée première et ses zéros
- la derivee seconde et ses zéros
- les points particuliers ( minimum, maximum, point d'inflexion etc ) je ne comprends pas tres bien non plus
- graphe de f ∩ avec l'axe oy
- graphe de f ∩ avec l'axe ox
- et le graphe
encore une fois, merci beaucoup pour l'aide que vous m'apportez !
-
mtschoon dernière édition par

Bonjour,
Les exercices précédents sont terminés maintenant.
Merci de donner les éléments de réponse que tu as trouvés, si tu as encore besoin d'aide.
Nous les vérifierons.
-
NNatsuDragneel dernière édition par
Bonjour.
Bah franchement, rien que le domaine je ne sais pas faire .. Je ne sais pas quoi prendre en compte pour une valeur absolue
-
mtschoon dernière édition par

Bonjour,
Pour tout x réel, quel que soit le signe de x(x-1), sa valeur absolue est ........donc la racine carré existe donc l'ensemble de définition de la fonction est ...............
(Complète)
-
NNatsuDragneel dernière édition par
Hmm je pense que le domaine est tout les réels ?
-
mtschoon dernière édition par

oui, c'est ça.
Pour tout x réel, quel que soit le signe de x(x-1), sa valeur absolue est positive (au sens large) donc la racine carré existe donc l'ensemble de définition de la fonction est R
Essaie de poursuivre.
-
NNatsuDragneel dernière édition par
Donc disons que pour les zéros de f' ( par exemple ) , même si je trouve une valeur négative, elle sera positive ?
-
mtschoon dernière édition par

Ta phrase n'a guère de sens...
Avant de parler des zéros de f', il faut calculer la dérivée (en supprimant d'abord les symboles de valeurs absolues - tu as dû voir cela dans ton cours -car il n'y a pas de formules de dérivées avec des valeurs absolues)As-tu fait la parité?
Comme je te l'ai déjà dit, on cherche la parité éventuelle juste après la recherche de l'ensemble de définition.
Si, par chance, la fonction est paire ou impaire, on peut réduire l'ensemble d'étude de moitié et compléter ensuite.
Si la fonction n'est ni paire ni impaire, on doit étudier la fonction sur tout l'ensemble de définition.
-
NNatsuDragneel dernière édition par
Je ne sais pas comment faire la parité .
J'ai calculer les limites et on a 2 asymptotes oblique : en +∞ : y = x - 1/2 et
en -∞ : y = -x + 1/2
-
mtschoon dernière édition par

La parité se fait toujours de la même façon ( regarde la définition dans ton cours)
Tu exprimes f(-x) et tu le compares à f(x).
Ici, f est ni paire ni impaire.
On étudie donc f sur R.J'ignore tes calculs mais les asymptotes sont exactes.
-
NNatsuDragneel dernière édition par
Je suis sur téléphone c'est pour ça que je peux pas tout mettre sinon mon téléphone ferme de force et la recharge donc je perds tout
 , arh, je vais continuer à travailler à fond au lieue vous dérangez pour des petites choses qui reflètent un minimum de recherches, j'essayerai de la faire au complet, merci beaucoup !
, arh, je vais continuer à travailler à fond au lieue vous dérangez pour des petites choses qui reflètent un minimum de recherches, j'essayerai de la faire au complet, merci beaucoup !
-
mtschoon dernière édition par

Effectivement, ce serait bien pour toi que tu approfondisses ton cours pour avoir les bases nécessaires. C'est ça qui te bloque.
Si tu as besoin, donne tes réponses et nous vérifierons.
Bon travail !
-
NNatsuDragneel dernière édition par
bonsoir.
Après avoir vu certaines vidéo, j'ai essayer de retirer la valeur absolue et j'ai eu
: f(x) = √x(x-1)
Est-ce juste ?
-
mtschoon dernière édition par

Tu as dû mal comprendre car tout dépend de x...
PRINCIPE
|A|=A pour A ≥ 0
exemple pour comprendre : |3|=3
|A|=-A pour A ≤ 0
exemple pour comprendre : |-3|=-(-3)=3
Dans ton exercice, ill faut donc que tu déterminesle signe de x(x-1)=x²x, suivant x (c'est simple)
Pour x²-x ≥ 0
f(x)=x2−xf(x)=\sqrt{x^2-x}f(x)=x2−x
Pour x²-x ≤ 0
f(x)=−(x2−x)=−x2+xf(x)=\sqrt{-(x^2-x)}=\sqrt{-x^2+x}f(x)=−(x2−x)=−x2+x
-
NNatsuDragneel dernière édition par
Il faut alors que je fasse l'étude sur 2 fonctions ?
-
mtschoon dernière édition par

oui mais pas n'importe où.
Cherche pour quels réels x²-x ≥ 0
Sur cet ensemble tu utilises la première expression écrite de f(x)
Cherche pour quels réels x²-x ≤ 0
Sur cet ensemble tu utilises la seconde expression écrite de f(x)
-
NNatsuDragneel dernière édition par
Bonjour.
Donc pour :
f(x) = x²-x ≥ 0
= x(x-1)
x = 0 et x =1DomF f(x) ≥0 : ] -∞ ; 0 ] U [ 1 ; + ∞ [
Et pour :
f(x) = -(x²-1)
= -x(x-1)
x= 0 et x= 1Df f(x) ≤ 0 : [ 0;1]
-
mtschoon dernière édition par

C'est un peu ça mais il s'agitx²-x positif ou négatif
( tu mélanges avec f(x) ; faute de frappe ou confusion ?? )
Pour x ∈] -∞ ; 0 ] U [ 1 ; + ∞ [ $f(x)=\sqrt{x^2-x} \$
Pour x ∈[0,1] f(x)=−x2+xf(x)=\sqrt{-x^2+x}f(x)=−x2+x
-
NNatsuDragneel dernière édition par
C'est juste que je ne savais pas quoi mettre mais ce que j'ai compris c'est que je ferai 2 dérivées première , etc c'est ça ?
-
mtschoon dernière édition par

oui.
Tu calcules la dérivée pour x ∈] -∞ ; 0 ] U [ 1 ; + ∞ [
Tu calcules la dérivée pour x ∈[0,1]
-
NNatsuDragneel dernière édition par
Bonjour.
- Pour x ∈ ] - ∞ ; 0 ] U [ 1 ; + ∞[
⇒ f'(x) = 2x-1/ √x²-x ⇒ zéros en 1/2
( on le prend car Df' = ]-∞ ; 0 [ u ] 1 ; +∞[ )
- pour x ∈ [ 0;1 ]
⇒ f'(x) = -2x -1/ √-x²+x ⇒ zéro en 1/2
( on le prend pas car il n'est pas compris dans le domaine Df : ] 0;1[ )
Donc pour x ∈ [0;1] , f' n'a pas de zéro
-
NNatsuDragneel dernière édition par
Ensuite,
- pour x ∈ ] -∞ ; 0] U [ 1 ; + ∞ [
F"(x) = (2x-1)'.(√x²-x ) - (2x-1).(√x²-1)' / (√x²-x )²
= 2.(√x²-x) - (2x-1)²/(√x²-x) / (√x²-x)²
= (2x²-2x) - (2x-1)² / (x²-1).(√x²-x)
= 2x²-2x -4x²-2 / (x²-x).(√x²-x)
Je n'ai pas continuer car je ne suis pas sûr de ce que j'ai fait .. Merci beaucoup !

-
mtschoon dernière édition par

Etourderies ?
Revois à nouveau la dérivée d'une racine carrée. Tu as oublié le "2" au dénominateur
En plus, tu as mis le contraire de ce qu'il faut...
Pour x ∈ ] - ∞ ; 0 ] U [ 1 ; + ∞[ f' n'a pas de zéro car 1/2 ne convient pas
Pour x ∈ [0,1) f' a un zéro (1/2) (qui convient)
Pense à Df' :
Df'=R-{0,1} ( car dénominateur non nul)
Pour la dérivée seconde : Df"=R-{0,1} ( car dénominateur non nul)
Pour le calcul, ce ne sera jamais bien beau mais comme la dérivée première est inexacte, la dérivée seconde aussi....
Je vais te mettre un lien où tu peux vérifier toi même dérivée première et dérivée seconde
*Bien sûr, tu n'es pas obligé d'exprimer les dérivées comme le logiciel, c'est seulement un outil de vérification. *
-
mtschoon dernière édition par

Regarde ici
http://www.formaltools.com/derivativecalculator.php
la racine carrée se note sqrt
Dans un cas,
en tapant
sqrt(x^2-x)
tu obtiens la dérivée première
en tapant
sqrt(x^2-x),2
tu obtiens la dérivée seconde
Dans l'autre cas,
en tapant
sqrt(-x^2+x)
tu obtiens la dérivée première
en tapant
sqrt(-x^2+x),2
tu obtiens la dérivée seconde
Bons calculs.
-
NNatsuDragneel dernière édition par
Mais c'est génial ça !!! Merci énormément ! Par contre pour f" il me laisse sous forme de racine ^^'
-
mtschoon dernière édition par

Le logiciel fait comme il a été programmé !
Tu as pu remarquer que pour les dérivées premières, il y a eu une simplification par 2.
Pour les dérivées secondes, si tu le souhaites, tu peux faire des réductions au même dénominateur.
A toi de voir...je ne m'en occupe pas...
-
NNatsuDragneel dernière édition par
Bon... Je n'arrive vraiment pas à calculer f" ... Je me perds dans mes calculs etc pfff
-
mtschoon dernière édition par

Méthode : tu pars de f' et tu dérives avec la formule de dérivée d'un quotient.
Tu transformes à ta guise, mais le résultat ne sera jamais beau...A toi de faire ; Ici, on aide à faire mais on ne fait pas ( et je crois que j'ai fait déjà beaucoup...)
Bonne fin de révisions.
-
NNatsuDragneel dernière édition par
Oui franchement sans vous j'aurez sûrement rater d'avance ! Merci beaucoup pour votre aider et pour tout ce que vous m'avez apporter !
-
NNatsuDragneel dernière édition par
Bonsoir ! Je voulais vous demandez .. J'ai établie le Tableau de signe de f' et j'ai déduis que la courbe de F(x) est positif jusqu'à 1/2 et est à nouveau positif par la suite
-
mtschoon dernière édition par

Le tableau de variation général (relatif aux deux expressions de la fonction) doit correspondre à la représentation graphique :
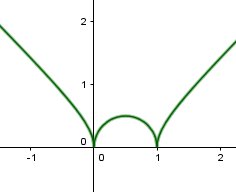
Tu peux ajouter les deux asymptotes, bien sûr.