Problèmes avec f' et f" pour f(x)=racine(x^2-x^4)

Bonjour !

J'ai comme exercice de dériver cette fonction :

F(x) =√x² $x^4$

DomF = [ -1 ; 1 ]

( pas d'asymptotes )

F'(x) = 2x -4x³ / 2√x² $x^4$
= 2x(1-2x²) / 2√x² $x^4$

DomF' : ]-1 ; 1[

Zéros : x = 0 et x = ±√1/2

Pour f" j'ai trouver $12x^{4 + 8x[sup]6}$

Zéros :

x = 0 et x= ±√3/2

Et j'aimerai savoir si vous pourrez vérifier f" s'il vous plait parce que quand je dresse mon tableau de variation , il y a un problème au niveau des concavités par rapport au signe de la courbe merci !

Bonjour,

Df est exact

f'(x) est exact mais tu peux simplifier par 2 :

$f'(x)=\frac{x-2x^3}{2\sqrt{x^2-x^4}$

Attention à Df' .

La condition est

$x2−x4>0x^2-x^4 \gt 0$

En factorisant :

$x^2(1-x^2) > 0$

Fais le tableau de signe et tu obtiendras : x ∈ ]-1,0[ ∪ ]0,1[

Df'=]-1,0[ ∪ ]0,1[

0 est donc à supprimer parmi les zéros de f' que tu as indiqués

Pour f" (méthode vue dans un précédent exercice), je suppose que c'est seulement le numérateur que tu as donné ( et sans simplification)

En simplifiant au mieux

$f′′(x)=−3x4+2x6x2−x4(x2−x4)f''(x)=\frac{-3x^4+2x^6}{\sqrt{x^2-x^4}(x^2-x^4)}$

$f′′(x)=x4(−3+2x2)x2−x4(x2−x4)f''(x)=\frac{x^4(-3+2x^2)}{\sqrt{x^2-x^4}(x^2-x^4)}$

Df"=]-1,0[ ∪ ]0,1[

0,±3/2 annulent bien le numérateur de f" mais ne conviennent pas car ils n'appartiennent pas à Df"

$\sqrt{\frac{3}{2}}\app 1.22$

f" n'a pas de zéros.

Merci beaucoup ! C'est un prof qui me l'a fait en plus mais c'est devenu indispensable de passer par vous, vous êtes au top ! Merci !

f' admet alors que ±√1/2 ?

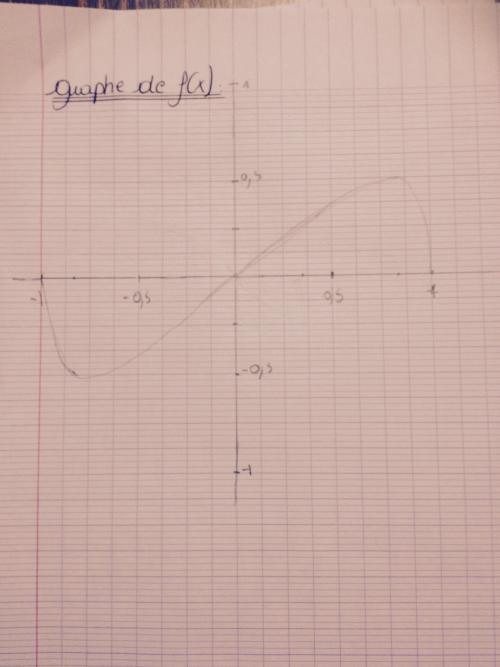Graphe de la fonction Le graphe ressemble donc à ca ?

oui, f' admet seulement deux zéros ±√(1/2)

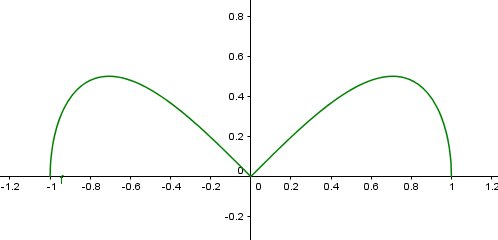
Par contre, pour le graphe, je ne pense pas que ce soit un prof qui te l'ait fait car il est faux...

Pour x ∈ [0,1], c'est bon mais sur [-1,0] c'est faux...

Je te laisse trouver la faute .

Non c'est moi qui l'ai fait , je pense que la courbe doit se trouver au dessus de l'axe des x ? En fait j'ai calculer f(-√1/2) pour avoir les coordonnées et j'ai teouver 1/2 mais c'est pas normal non ? Je ne sais pas ..

Effectivement, une racine carrée ne peut pas prendre des valeurs négatives donc sur ]-1,0[, ta courbe n'a pas de sens !

La courbe doit être l'illustration du tableau de variation (dérivée, son signe) donc je ne comprends pas comment tu pu faire une telle courbe (sauf si ton tableau de variation est faux aussi...)

En plus, la courbe que tu représentes a comme centre de symétrie le point O, ce qui correspond a une fonction impaire, or la fonction f est PAIRE (elle admet l'axe des ordonnées comme axe de symétrie).

Ah d'accord j'ai compris, je ferai la parité aussi, merci beaucoup

En principe, on fait la parité dès le début de l'étude, juste après l'ensemble de définition.

Si une fonction est paire, on peut faire l'étude seulement sur la moitié de l'ensemble de définition (ici [0,1]) et l'on complète le tableau de variation et la courbe en utilisant cette propriété.

(même idée si la fonction est impaire)

Cela simplifie le travail !