Domaine de définition d'une fonction trigonométrique 5

Bonjour , J'ai un examen de passage mais j'ai du mal à faire mes exercices , j'ai besoin d'aide afin que vous me corrigez svp. Merci

Comment faire pour calculer le Domaine de cette fonction
Dom : f(x)=√2cos2x+(2-2√3)cosx+2-√3 / Sin(x+2π/3) CE: 2cos2x+(2-2√3)cosx+2-√3 ≥ 0

2(cos²x-sin²x)+cosx(2-√3)+2-√3 ≥0
4cos²x-2+(2-√3)cosx+2-√3 ≥0
On pose cosx=x
4x²+(2-√3)x-√3 ≥0

Δ=(2-√3)²-4×4×(-√3)
=4-8√3+12+16√3
=(2+2√3)²
0: -1/2 ET √3 /2
Pour -1/2 on a : π/3 et -π/3
Pour √3/2on a : π/6 et -π/6

Sin(x+2π/3) ≠ 0
x≠2π/3 et 5π/3

Dom f: ]π/9+2Kπ; π/6+2Kπ] U ]2π/3+2Kπ; 5π/3+2Kπ]

Merci de me corriger
La racine comprend tout le numerateur de la fonction **

Bonsoir,

Toi aussi ?

Je regarde un peu.

Le début est bon.

Citation
Pour -1/2 on a : π/3 et -π/3
A revoir

Citation
Sin(x+2π/3) ≠ 0
x≠2π/3 et 5π/3
A revoir

Oui oui nous sommes dans la même classe sauf qu'on a pas les mêmes énoncé malheureusement , pour cosinus c'est :

x = π/3 et 5π/6 alors ?

Et sinus :

x ≠-2π/3 et π/3 ?

C'est bon pour sin(x+2π/3)=0

Revoir cosx=-1/2 ( faire le cercle trigonométrique et lire)

Remarque indiquée dans les topics précédents sur le même sujet:
Indiquer la période de f (ici 2π),
Indiquer sur quel intervalle I on travaille ([-π,π] ou [0,2π]
Trouver l'ensemble de définition sur l'intervalle I choisi
Généraliser à R en utilisant la période

Sur mon cercle trigonométrique et à la calculatrice je trouve π/3 et pareil quand j'fais arccos ( -1/2 )

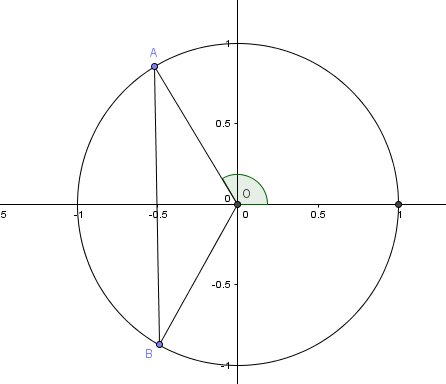
Visiblement, c'est de 1/2 dont tu parles et non de -1/2.

$fichier math$

Ma calculatrice devint folle :o, donc ça correspond à 2π/3 et -2π/3 ?

oui.

Il faut revois maintenant Df.

Df sur $mathbb{R}$ : ] -π/6 + 2kπ ; π/6 + 2kπ ] u [ 2π/3 + 2kπ ; 5π/6 + 2kπ [ u ] 5π/6 + 2kπ ; -2π/3 + 2kπ [ avec k ∈ $mathbb{Z}$

Ce 5π/6 est très bizarre...

Si l'on veut écrire correctement l'ensemble de définition sur [-π,π] , cela donne :

[-π/6,π/6] ∪ [-π,-2π/3[ ∪ [2π/3, π]

Sur R , c'est l'union de tous les ensembles du type [-π/6+2kπ,π/6+2kπ] ∪ [-π+2kπ,-2π/3+2kπ[ ∪ [2π/3+2kπ, π+2kπ], avec k ∈ Z

PS : Cela fait 5 exercices du même type...

Oui je sais, j'ai plus ou moins compris les autres mais le fait que c'était cosinus au numérateur et sinus au dénominateur ca m'embrouillait un petit peu , merci beaucoup pour votre aide