graphique de f(x)=racine de (x^4-x^2)

Bonjour !

J'aurai juste besoin d'une petite vérification du graphique s'il vous plait parce qu'il ne correspond pas à mon tableau de variation. Merci d'avance.

f(x) = √ $x^4$ -x²

f est paire.

DomF : ]-∞ ; -1 ] u[ 1 ; +∞[

Comportements aux bornes :

Pas d'asymptotes

f'(x) = 4x³-2x/2√ $X^4$ -x²

Zéros de f' : -√1/2 ; 0 et √1/2 que l'on prend pas car pas compris dans DomF'

f"(x) = ( en simplifiant)
= (2x²-1)' .(√x²-1) -(2x²-1).(√x²-1) / (√x²-1)²
= (4x³-4x) - (2x³-x) /(x²-1)(√x²-1)
= 2x³-3x /(x²-1). (√x²-1 )
Zéros : 0 et ±√3/2

Et mon problème, c'est que mon tableau de variation ( plus précisément a gauche de -1 ) pour f" est bizarre par rapport à mon graphe .. MERCI !!!!!

Merci de mettre un titre significatif

Bonsoir,

Fais attention au domaine de définition ( fais un tableau de signes de $x$ ^4 $x^2$ soigné)

Df=]-∞,-1] ∪ {0} ∪ [1,+∞[

Si c'est le graphique qu'il te faut , le voici

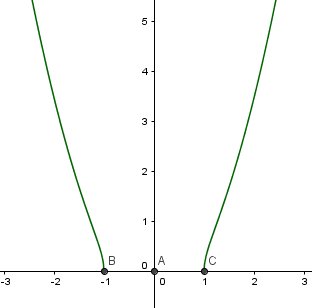
$fichier math$

D'accord merci, et mes zéros de f" sont correctes ? J'avais poster deux images mais je crois qu'elles n'ont pas été afficher. Je les avais mise car mon tableau de variation de correspondait pas au graphe ( concavité ) mais bon .. Merci énormément !

REMARQUES :

Ici, on ne peut pas poster deux fois le même sujet : les doublons ne sont pas permis, ce qui était le cas.
Un des deux topics a donc été supprimé.

De plus, tu es sur un forum public consultable par tous; les écritures et schémas joints doivent être "présentables".
Vu l'état de tes brouillons joints( !), j'ai supprimé le topic avec brouillons.

TON PROBLEME :

D'abord :
Df'=Df"=]-∞,-1[ ∪ ]1,+∞[

0 ne fait donc pas partie des zéros de f" (ni de f')

Ensuite :
Après simplifications, tes calculs de dérivées sont corrects mais seulement pour x positifcar dans les simplifications , √x² a été remplacé par x
Cela n'est valable que pourx positif (pour x négatif, √x²=-x)

En bref, ce que tu as fait est valable pour x positif c'est à dire sur ]1,+∞[ pour les dérivées (première et seconde)
Pour la concavité, "à droite de 1", comme tu dis, c'est bon, mais "à gauche de -1", ce n'est pas bon.

Je vais encore me répéter !

Vu que f est paire, tu aurais dû te contenter de faire l'étude de f,f',f" pour x POSITIF ( et l'écrire sur ta copie). Dans ce cas, les calculs effectués sont justes et la concavité sur ]1,+∞[ aussi.
Ensuite, sans faire de nouveau calculs, tu complètes par parité ( courbe symétrique par rapport à l'axe des ordonnées) et ainsi, il n'y a pas de problème de concavité sur ]-∞,-1[ .

Cela t'évite de refaire les calculs de f' et f" pour x négatif en remplaçant √x² par -x.

As-tu compris ?

Bonjour.

Justement le topic que vous avez supprimer était : f(x) = √x² $x^4$

Fin bref c'est pas grave vu que l'autre je l'ai terminer. Oui j'ai bien compris merci beaucoup !

Et non, tu te trompes...

Le topic "doublon" mis à la poubelle est sorti de la poubelle provisoirement pour que tu puisses constater qu'il s'agit bien d'un doublon (avec des brouillons) relatif à√(x^4-x^2).

(quand je parle de "suppression", il s'agit d'une "mise à la poubelle")

Ensuite, ce doublon sera remis à la poubelle.

Le topic sur**√(x^2-x^4)**que tu as appelé :problèmes avec f' et f" est toujours à sa place bien sûr !
Tu n'avais pas choisi un titre pertinent : je vais compléter le titre pour t'éviter toute confusion !

Bon travail ( et évite les confusions ! )

Le doublon concerné relatif à√(x^4-x^2) est retourné à la poubelle..

Bonne fin de révision.