Conjecturer et démontrer la nature d'un quadrilatère

Bonjour à tous, dans un DM, je bloque sur un exercice de géométrie, voici l'énoncé :

ABCD est un parallélogramme de centre O.
On construit les points E,F,G et H à l'extérieur du parallélogramme tels que E soit sur (AB); F sur (BC); G sur (CD); H (DA); et vérifiant BE=CF=DG=AH.

1)Faire une figure
2)Quelle est la nature du quadrilatère EFGH?
3)Démontrer la cconjecture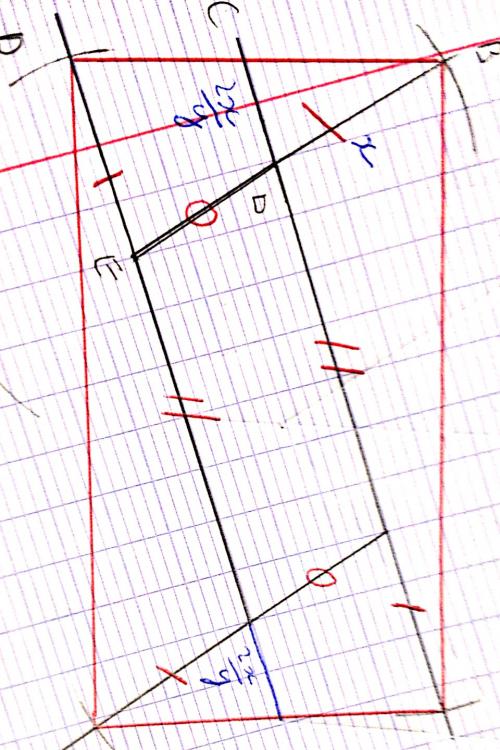

Schéma de la figure avec quelques annotations.

J'ai d'abord eu beaucoup de mal à faire la figure, au début EFGH était un losange mais en retracant ma figure de manière plus grande et plus précise, j'ai fini par obtenir un rectangle.
Comme j'avais affaire à deux droites coupées par une sécante, j'ai utilisé la propriété des angles alternes-internes et correspondants...sans succès.
J'ai également tenté le théorème de Thalès...sans succès.

Pouvez-vous m'aider? Merci de vos réponses!

Bonjour,

Bien sûr, tu peux obtenir des cas particuliers ( losange, rectangle,...) mais de façon générale, EFGH est un parallélogramme.

Pour le prouver, si tu connais, en utilisant les vecteurs, c'est facile.

En décomposant avec la relation de Chasles, tu peux prouver que
$HE⃗=GF⃗\vec{EF}=\vec{HG} \ \vec{HE}=\vec{GF}$

Bonjour et merci de votre réponse,

Les vecteurs permettent bien de trouver la solution mais nous ne les avons pas encore étudiés.

Cependant, il existe une autre méthode, certes plus longue pour trouver le résultat.

Il faut prouver que AECB et HBCD sont des parallélogrammes (Les côtés opposés sont parallèles et égaux). Comme ce sont des parallélogrammes, leur diagonales se coupent en leur milieu donc HO = OF et EO = BO.
Du coup, cela signifie que les diagonales du quadrilatère EFGH se coupent en leur milieu et donc que EFGH est un parallélogramme!

Faute de vecteurs, ton idée est un peu lourde, certes, mais parait très bonne !