Mettre un problème sous forme de suite et le résoudre

Bonsoir, je suis en terminale S et j'ai un dm de maths a rendre pour mercredi et j'ai réussi a faire 2 exercices sur 3 il y a en a un ou je bloque vraiment si vous pourriez m'aider sa serait vraiment super svp je vous poste l'exercice merci d'avance a ceux qui m'aideront

L'étang d'Igor:
Igor a fait l'acquisition d'un petit rang non loin de chez lui qu'il décide de rempoissonner en 2014 car il est vide. Il achète alors 2000 petit goonchs pour son étang.
Le nombre de poissons est reduit de 20% a cause des crues tous les ans. Heureusement, chaque année, 200 nouveau petit goonchs naissent
On note Un le nombre de goonchs dans l'étang lors de l'année 2014+n. Ainsi U0=2000

Combien de poissons y a-t-il dans l'étang cette année (2015)?L'année prochaine?
2)Montrer que pour tout n∈ entier naturel,Un+1= 0.8Un+200
3)Conjectures sur la suite (Un)
a)Representer U0, U1, U2, U3 et U4 sur un repere
b)Quel semble etre le sens de variation de la suite (Un)? Sa limite?
4)On considère la suite (Vn) définie pour tout n∈ entier naturel par: Vn=Un-1000
a)Montrer que (Vn) est une suite géométrique, dont on donnera le premier terme et la raison
b)En deduire une expression de Vn en fonction de n
c)En deduire une expression de Un en fonction de n
d)Quelle est la limite de la suite (Un)?
5)Combien y aura-t-il de poissons dans l'étang d'Igor au bout d'un très très très grand nombre d'années?

Je vais vous mentir mais je n'ai vraiment rien compris donc si vous pourriez m'expliquez et m'aider sa serait super et les autres exercices du Dm ne se ressemble pas du tout a celui la :frowning2:
J'ai réussi a faire quelque question mais je suis pas sure du résultat

Merci de mettre un titre significatif

Bonsoir,

Piste pour démarrer :

En 2014: $U_0$ =2000

En 2015 : $U$ 1 $= U$ {0-} $2020%U_0$ +200=(1-0. $2)U_0$ +200=0. $8U_0$ +200

Tu comptes

Avec la même démarche,

$U$ _{n+1} $= U$ _n $−20-20%U_n$ +200=(1-0. $2)U_n$ +200=0. $8U_n$ +200

Le principe de la représentation de $U_0$ , $U_1$ , $U_2$ , $U_3$ ,...a dû être vu dans ton cours.

Pour une explication complémentaire, tu peux regarder ici :

http://www.mathforu.com/cours-93.html

Pour ce qui est de la suite à étudier, tu devrais trouver un schéma qui correspond à celui ci (tu places le point d'abscisse $U_0$ =2000 sur l'axe des abscisses et tu fais la construction à partir du point (2000,0).

$< s t r o n g > U$ _{n+1} $f(U_n$ )
La représentation graphique de f (en trait plein) est ici la droite d'équation y=f(x)=0.8x+200
La droite en pointillé est la droite d'équation y=x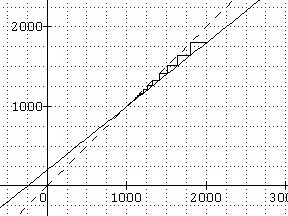

$fichier math$

Si tu as besoin, indique ta conjecture et nous vérifierons.

Merci beaucoup mtschoon es ce que je peux te poster mes reponses de la fin de l'exercices pour que tu me dises si j'ai bon?

Oui, tu peux.

? ? ?