Algorithme-Dichotomie

Bonjour, n'ayant jamais fait d'algorithme, j'espère que vous pourrez m'aider à faire ce devoir maison. Merci d'avance !

On considère l'algorithme suivant :

Variables : a, b, m
a prend la valeur 1
b prend la valeur 2
Tant que b – a > 0,1
m prend la valeur (a+b)/2
Si m² - 2 > 0 alors
b prend la valeur m
Sinon
a prend la valeur m
Fin si
Fin Tant que
Afficher a
Afficher b

a) Compléter le tableau suivant donnant les différentes étapes de l'algorithme : (la copie de ce tableau est impossible ...)
colonnes : (vide) / m / a / b / a-b
ligne : (vide) / Etape 1 / Etape 2 ...

b) Que fait cet algorithme ?

c) Modifier l'algorithme de manière à pouvoir choisir l'amplitude de l'encadrement obtenu.
Programmer cet algorithme à l'aide d'un logiciel ou de la calculatrice et le tester.

d) On veut maintenant obtenir un encadrement de la solution négative de l'équation .
Pour cela on donne à a et b les valeurs respectives -2 et -1. L'algorithme fonctionne-t-il ?
Pourquoi ?

e) Modifier la condition de l'instruction « si … alors » de manière à ce que l'algorithme donne la réponse correcte.

2 a) Conjecturer à l'aide de la calculatrice le nombre de solutions de l'équation .

b) Modifier l'algorithme précédent de manière à obtenir un encadrement d'amplitude 10-2 de la solution positive de cette équation, puis de chacune des solutions conjecturées.

Merci de mettre des titres significatifs.

Bonjour,

Pour comprendre ce que fait cet algorithme, tu dois l'utiliser étape par étape en complétant le tableau.

Il doit y avoir une ligne**"initialisation"** avec a=1, b=2 et b-a=1

Dans l'étape 1:
m=1.5, tu calcules m²-2 (tu trouves m²-2 >0) donc b=1.5 et a=1 ; b-a=0.5

Tu continues ainsi tant que la condition b-a > 0.1 est réalisée.

Lorsque tu auras terminé de compléter le tableau, tu comprendras que les valeurs finales de a et b te permettent d'encadrer la solution positive (√2) de l'équation x²-2=0, à 0.1 près.

Cette méthode est appelée DICHOTOMIE.
Tu peux faire des recherches sur le web pour avoir des informations.

J'ai tapé l'algorithme du 1) sur AlgoBox.
Il affiche a=1.375 et b=1.4375
Sauf erreur, ce sont les dernières valeurs de a et b que tu dois trouver dans ton tableau.

Si ça peut t'être utilise, je te joins le programme modifié fait avec AlgoBox pour que l'utilisateur choisisse l'amplitude e de l'encadrement obtenu.
Evidemment, tu le fais avec le logiciel ou la calculatrice de ton choix.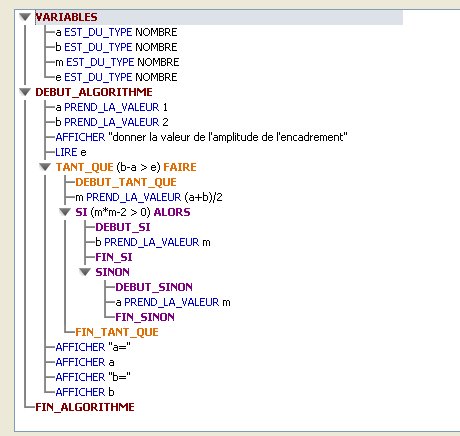

$fichier math$

Pour e=0.1, le programme répond a=1.375 et b=1.4375 (normal vu que ce sont les réponses du programme précédent)
Pour e=0.01, le programme répond a=1.4140625 et b=1.421875

Bon travail.