Inéquation du second degré
-
DDANYBOONE59 dernière édition par
bonjour,
je dois résoudre cette inéquation, mais je ne suis pas très doué en maths,
-x²+5x-4≤0
pourriez vous m'expliquer le mieux possible afin que je comprenne, comment procéder
remerciements
danyboone59 :frowning2:
-
EEmeraude_S dernière édition par
Bonjour,
Sais-tu résoudre une équation du second degré ? Sais-tu calculer le discriminant d'une équation du second degré ?
-
DDANYBOONE59 dernière édition par
Emeraude_S
Bonjour,Sais-tu résoudre une équation du second degré ? Sais-tu calculer le discriminant d'une équation du second degré ?
oui discrimiant delta = b²-4ac
delta=(-1)²-4(-1)x3
delta=1+12
delta=13>0 donc deux solutions
x1=-b-√delta/2a et x2=-b+√delta/2a
x1=(-4-√13)/2 x2=(-4+√13)/2
x1=-(4+√13)/2est ce cela?
-
Mmathtous dernière édition par
Bonjour à tous deux.
Danyboone59 : juste un petit conseil.
Il est souvent désagréable d'avoir un polynôme dont le premier coefficient est négatif.
Comprends-tu que ton inéquation peut s'écrire : x² - 5x + 4 ≥ 0 ?
-
Mmathtous dernière édition par
Citation
delta=(-1)²-4(-1)x3Peux-tu expliquer d'où vient ce "3" ?
Le début étant faux, le reste aussi.
De plus, il y a confusion quant aux lettres (a,b,c).
-
EEmeraude_S dernière édition par
Oui le discriminant est bien delta=b2−4<em>a</em>cb^2-4<em>a</em>cb2−4<em>a</em>c mais avec pour équation ax2+by+c=0ax^2+by+c=0ax2+by+c=0
Tu t'es trompé en identifiant b.
Une fois que tu as calculé ton discriminant tu doit effectuer un tableau de signe.
-
DDANYBOONE59 dernière édition par
Emeraude_S
Oui le discriminant est bien delta=b2−4<em>a</em>cb^2-4<em>a</em>cb2−4<em>a</em>c mais avec pour équation ax2+by+c=0ax^2+by+c=0ax2+by+c=0Tu t'es trompé en identifiant b.
Une fois que tu as calculé ton discriminant tu doit effectuer un tableau de signe.
donc -x²+5x-4≥o revient à écrire x²-5x+4≥0
je cherche le discriminant
delta= 5²-4(-1)(-4)
delta=25+16
delta=41
delta >à o donc calculer x1 = (-b-√delta)/2a
et x2=(-b+√delta)/2a
soit x1=(5-√41)/2 et x2= (5+√41)/2est ce cela? jusque maintenant? svp
-
EEmeraude_S dernière édition par
Tu as fait une erreur de calcul :
Delta= 25-4*(-1)(-4)=25-4*4=25-16=9
-
EEmeraude_S dernière édition par
Ensuite tu as : Δ>0
Donc, tu calcules ses deux racines.
-
DDANYBOONE59 dernière édition par
Emeraude_S
Tu as fait une erreur de calcul :
Delta= 25-4*(-1)(-4)=25-4*4=25-16=9oui erreur de signe ok merci
donc x1(=5-√9)/2
x1=1x2=(5+√9)/2
x2=4est ce bon?
par contre je n'arrive pas à comprendre ce que je dois donner comme solutions, je dois regarder le tableau de signe mais je ne sais pas faire.....
-
EEmeraude_S dernière édition par
Oui c'est exact.
Maintenant tu étudie le signe du polynôme x2−5x+4x^2-5x+4x2−5x+4
-
EEmeraude_S dernière édition par
Une fois ton tableau de signe fait, tu regardes sur quelle partie x2−5x+4x^2-5x+4x2−5x+4 est superieur ou egal à 0.
-
DDANYBOONE59 dernière édition par
Emeraude_S
Une fois ton tableau de signe fait, tu regardes sur quelle partie x2−5x+4x^2-5x+4x2−5x+4 est superieur ou egal à 0.j'ai beaucoup de mal avec le tableau de signe, pouvez vous me l'expliquer?
merci
danyboone59
-
DDANYBOONE59 dernière édition par
Emeraude_S
Une fois ton tableau de signe fait, tu regardes sur quelle partie x2−5x+4x^2-5x+4x2−5x+4 est superieur ou egal à 0.j'ai beaucoup de mal avec le tableau de signe, pouvez vous me l'expliquer?
merci
danyboone59
-
EEmeraude_S dernière édition par
Oui, je vais essayer de t'expliquer.
Tu sais, je suppose que la première ligne du tableau concerne les valeurs que prend x, et les suivantes concernes les fonctions (ici, le polynôme) que tu étudies ?
Ceci est le tableau de signe vide. Il faut maintenant le calculer.
Tu as calculé les valeurs de x où ton polynôme s'annule, il faut les faire apparaître. Sais-tu comment les représenter ?
-
DDANYBOONE59 dernière édition par
Emeraude_S
Oui, je vais essayer de t'expliquer.
Tu sais, je suppose que la première ligne du tableau concerne les valeurs que prend x, et les suivantes concernes les fonctions (ici, le polynôme) que tu étudies ?
Ceci est le tableau de signe vide. Il faut maintenant le calculer.
Tu as calculé les valeurs de x où ton polynôme s'annule, il faut les faire apparaître. Sais-tu comment les représenter ?oui ça me donne
x²-5x+4 + 0 - 0 +
-
EEmeraude_S dernière édition par
Oui c'est bien ce que tu obtiens.
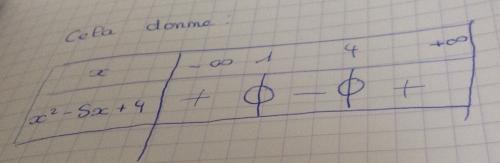
Donc, maintenant, il ne te reste plus qu'à lire le tableau pour resoudre ton inéquation.
x2−5x+4x^2-5x+4x2−5x+4≥0
Tu cherches les intervalles ou le polynôme est positif donc les intervalles solutions sont ceux où il y a le signe"+"
S=]-∞;1]∪[4;+∞[As-tu compris ?