Donner le quotient d'une division euclidienne

bonjour à tous;

la question est:
quel est le quotient de la division euclidienne pour:

x^3 + 2x^2+1 par x^3+x+1 -> j'ai trouvé Q=1

x^2-x+1 par 2x+2 -> j'ai trouvé Q=1/2x-1/2

x^3+x^2+1 par x^2+x+2 -> j'ai trouvé Q=x+1

x^3+3x^2-x+1 par x^3+1 -> j'ai trouvé Q=1

Le début est-il juste SVP?

merci

Bonjour,

Je m'excuse d'insister mais je ne peux poursuivre mon DM sans cette partie.

Merci vraiment pour votre aide.

Bonjour,

Désolée ; on aide (bénévolement, dans les limites de nos disponibilités), mais on ne peut pas vérifier toujours toutes les réponses...
C'est à ton professeur de les vérifier!

Je regarde.

La première et la dernière sont exactes.

Revois les deux autres.

Bonjour MTSCHOON

Il n y a pas de soucis je sais que vous faites ça bénévolement et c'est très honorable.
Concernant mon prof de maths c'est compliqué car nous avons depuis quelques jours un nouveau prof qui est chinois qui maîtrise pas très bien le français de plus il part très rapidement à la fin du cours donc je ne peux pas lui poser mes questions.

Je risque encore de vous demander quelques conseils pour ce chapitre.

Passer un bonne journée.

Bon courage, dut !

Je te mets les réponses que tu dois trouver pour la deuxième et la troisième division.

Pour la deuxième

$q=12x−1q=\frac{1}{2}x-1$

Pour la troisième :

$q = x$

Bons calculs.

Merci beaucoup de votre aide.

je des exercices ou je dois maintenant trouver le reste je vais m'entrainer dessus.

Bonsoir,

je ne comprends pas pour la troisieme question:

Quand j'ai X en quotient, j'ai 2x+1 en reste hors ne faut-il pas qu'il n'y est plus de X au niveau du reste?

bonne soirée

Pour la troisième, le reste est 1-2x

Tu ne peux pas faire plus car le degré du diviseur est supérieur au degré du reste.

Je viens de refaire l'exercice, et j'ai eu juste je pense avoir compris.

Merci beaucoup

De rien .

Je trouve pour X^2-X+1 par X+2 -> R=7

pour X^3-X^2+1 par X^3+X+1 -> R= -X^2-X

pour X^2+1 par 2X^2+2 -> R=1

Bonne soirée

Les deux premiers restes sont justes.

Revois le troisième.

Merci beaucoup MTSCHOON je suis sur la bonne voie

Bonjour,

Après avoir refais le calcul du troisième je trouve R=0

Par contre j'ai quelques problèmes avec 3 autres calculs du même type.

pour X^3+x^2+1 par 3x^3+x^2+x+2
quand je mets 1/3 en quotient je tombe sur le reste -> -1/3 +1/3x +2/3+1 quand je regarde les réponses proposées il y a : R=2/3x^2 - 1/3x +1/3
j'ai beau refaire le calcul je tombe sur le même résultat.

Nous verrons plus tard pour les 2autres calculs, je préfère comprendre mes erreurs avant.

merci à tous et bon week-end.

Oui R=0

Pour ta dernière question :

Recompte ton calcul car le reste proposé par ton QCM est exact.

Merci beaucoup mais je ne retombe pas sur la bonne réponse.

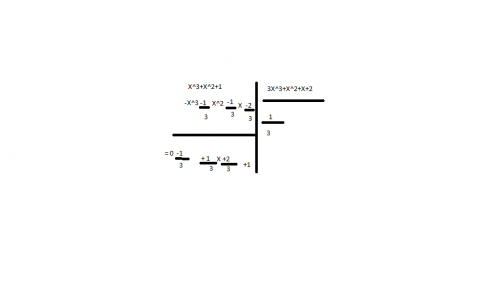
$fichier math$

c'est pas terrible mais ca peut aider.

je dois passer à cote de quelque chose.

Il semble que c'est lorsque tu fais la somme pour obtenir le reste que c'est faux

Termes en $x^3$ : $x$ ^3 $x^3$ =0

Termes en $x^2$ : $x$ ^2 $- (1 / 3) x$ ^2 $2/3)x^2$

Termes en x : 0x-(1/3)x=-(1/3)x

Termes constants: 1-(2/3)=+(1/3)

D'où :

$r=23x2−13x+13r=\frac{2}{3}x^2-\frac{1}{3}x+\frac{1}{3}$

Merci beaucoup j'ai compris sauf pour le x^2 je n'arrive vraiment pas à voir pourquoi le résultat est 2/3x^2

$x2−13x2=(1−13)x2=(33−13)x2=3−13x2=23x2x^2-\frac{1}{3}x^2=(1-\frac{1}{3})x^2=(\frac{3}{3}-\frac{1}{3})x^2=\frac{3-1}{3}x^2=\frac{2}{3}x^2$

Merci beaucoup j'ai compris.

De rien !