Etudier le signe de variation d'une fonction trigonométrique avec valeur absolue

bonjour!.. j'ai la fonction f(x) = |xsinx - cosx| x E [-2pi,pi] et j'ai posé g(x) = xsinx - cosx

je dois trouver le signe de g(x) sur [-2pi,pi] pour enlever la valeur absolue, pour cela j'ai cherché les racines de g(x) mais en transformant un peu la fonction j'suis arrivé à xtanx=1 qui me semble difficile à resolver .. j'ai aussi calculé g'(x) qui est égale à 2sinx + xcosx mais toujours sans issue.. quelques astuces de votre part m'aideraient beaucoup.. merci

Bonjour,

Je vois que tu as déjà posté ton énoncéailleurs et que tu as obtenu des réponses...mais avec cet énoncé, je crains que tu ne puisses pas avoir des réponses pertinentes, ni ici, ni ailleurs...

Es-tu vraiment certain de cet énoncé ?

L'ensemble d'étude est surprenant .

Par exemple, [-∏,∏] aurait été mieux.
Vu que la fonction g est est paire, l'étude sur [0,∏] suffirait.

D'ailleurs, cette fonction g elle-même est bizarre.

Si par exemple, g(x)=xsinx+cosx ou bien g(x)=xcosx-sinx, alors le signe de g'(x) est trouvable simplement, les variations de g aussi et avec le théorème des valeurs intermédiaires, le problème peut se régler facilement.

Mais, avec l'expression de g(x) que tu as écrite, cette méthode ne donne rien de bien...

Avec un tel énoncé, on ne peut rien faire de bien rigoureux...

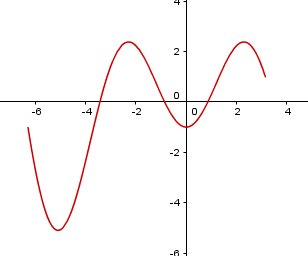
Si tu veux la représentation graphique de le fonction g dont tu as parlé dans ton énoncé écrit, la voici.

Bien sûr, tu peux toujours faire une lecture graphique, mais il faudrait que ce soit indiqué dans l'énoncé...

$fichier math$

je vois.. merci^^

De rien mais comme déjà dit, vérifie ton énoncé...