Sens de variations 3

Bonjour,
J'essaie de faire cet exercice :
Soit s(t)= t/2 + 3 + ln(t)
Pour t/2 cela correspond t il au domaine de définition de l'inverse?
Comment faire pour le vu que nous n'avons pas de valeurs comme vu précédemment ?

Merci de votre aide

Bonjour,

Je me demande si tu ne confonds pas t / 2 avec 2 / t

Tout dénominateur doit être non nul ( car la division pas 0 n'existe pas)

Pour t/2, le dénominateur vaut 2 : il est nécessairement non nul

aucune condition d'existence pour t / 2

3 est une constante : aucune condition d'existence pour 3

on ne peut prendre le logarithme que d'un nombre strictement positif

Pour ln(t), la condition d'existence est t > 0

Bilan : la sommes s(t) existe si et seulement si t > 0

$strong>D_S$ =]0,+∞[

Merci MTSCHOON et merci de votre aide.

Si je comprends bien la dérivée est égale à t/2 + 1/x

Non ...

$t2=12t\frac{t}{2}=\frac{1}{2}t$

Revois les formules relatives aux dérivées.

Lorsqu'on a le produit d'une constante par une fonction, la dérivée est le produit de la constante par la dérivée de la fonction.

$(12×t)′=12×(t)′=12×1=12(\frac{1}{2}\times t)'=\frac{1}{2}\times (t)'=\frac{1}{2}\times 1=\frac{1}{2}$

la dérivée de ln(t) n'est pas 1/x vu que la variable est t ; c'est 1/t

$(ln(t))′=1t(ln(t))'=\frac{1}{t}$
Conclusion :

$s′(t)=12+1ts'(t)=\frac{1}{2}+\frac{1}{t}$

1/2 >0et
1/t >0
Donc la fonction est croissante ?

Oui.

Détaiile un peu plus :

Sur $D_S$ , t > 0 donc 1/t > 0

Vu que 1/2 > 0, la somme 1/2+1/t > 0 donc s'(t) > 0 donc
s croissante (strictement)

Merci MTSCHOON, nous allons voir si j'ai compris.

Soit s(t)= -t/5 + 3 + ln(t)

Pour ln(t), la condition d'existence est t>0 soit ]o, +infini[
Pour -t/5, la condition d'existence

La dérivée est s'(t)= -1/5 + 1/t
Donc -1/5 <0
1/t >0
Par contre je ne sais pas ce que peut donner la somme de -1/5 + 1/t car nous avons une fonction croissante et l'autre décroissante.

Néanmoins la réflexion est elle bonne?

Citation
Pour -t/5, la condition d'existence
La phrase ne doit pas âtre terminée...(pas de condition d'existence)

Il faut conclure : $D_s$ =]0,+∞[

s'(t) est bonne.

Citation
nous avons une fonction croissante et l'autre décroissante.
Il ne s'agit pas de cela.
Il y a un terme négatif et un terme positif.

Comme tu ne peux pas avoir directement le signe de cette somme, tu réduis au même dénominateur

Sauf erreur de ma part cela donne:

-1t/5t + 6/5t

D'où sort ce "6" ? rectifie

Ensuite, il faut ajouter pour que ça puisse servir.

-1/5 + 1/t

-1t/5t + 15/5t

= -1t/5t + 5/5t

Par contre je ne peux pas faire la somme de -1t + 5

Bizarre ce que tu dis...

$s′(t)=−t5t+55t=−t+55ts'(t)=\frac{-t}{5t}+\frac{5}{5t}=\frac{-t+5}{5t}$

Lorsque tu auras compris, il faudra étudier le signe de s'(t) pour t ∈ ]0,+∞[

-t+5/5t est une fonction négative.
La fonction est donc strictement décroissante.

Non.

Pour t ∈ ]0,+∞[ , t > 0 donc 5t > 0

Le signe de (-t+5) / (5t) est donc du signe de -t+5

-t+5 < 0 <=> -t < -5 <=> t ................(complète)

-t+5 > 0 <=> -t > -5 <=> t ................(complète)

-t+5 = 0 <=> -t = -5 <=> t ................(complète)

Pour t ∈ ]0,+∞[ , t > 0 don 5t > 0

Le signe de (-t+5) / (5t) est donc du signe de -t+5

-t+5 < 0 <=> -t < -5 <=> t>-5/-1=5 la fonction est croissante

-t+5 > 0 <=> -t > -5 <=> t < -5/-1=5 la fonction est croissante

-t+5 = 0 <=> -t = -5 <=> t= 5

J'espère que cela était ce qui était demandé.

Il y a une erreur.

La fonction n'est pas toujours croissante. Revois ce que tu as écrit.

Je pense l'avoir identifié.

-t+5 > 0 <=> -t > -5 <=> t < -5/-1=5 la fonction est décroissante.

Donc la fonction atteint un maximum en 5.

non.

écris plus clairement (on n'écrit pas des égalités au milieu d'inégalités) ;
c'est incorrect et source d'erreurs.

Reprends clairement

-t+5 < 0 <=> -t < -5 <=> t > 5 la fonction est ....

-t+5 > 0 <=> -t > -5 <=> t < 5 la fonction est ....

-t+5 = 0 <=> -t = -5 <=> t = 5 la fonction admet un ....

-t+5 < 0 <=> -t < -5 <=> t > 5 la fonction est CROISSANTE

-t+5 > 0 <=> -t > -5 <=> t < 5 la fonction est DÉCROISSANTE

-t+5 = 0 <=> -t = -5 <=> t = 5 la fonction admet un MAXIMUM EN 5

Reprenons...

Si tu as compris (?), s'(t) est du signe de -t+5(revois les messages précédents )

s'(t) < 0 <=> -t+5 < 0<=> -t < -5 <=> t > 5
la fonction est DECROISSANTE

s'(t) > 0 <=> -t+5 > 0 <=> -t > -5 <=> t < 5
la fonction est CROISSANTE

-t+5 = 0 <=> -t = -5 <=> t = 5
la fonction admet un MAXIMUM EN 5

Merci MTSCHOON,

Malgré tout si t>5 vu que c'est supérieur à 5 la fonction ne peut que augmenter donc être croissante alors que quand t<5 la fonction aurait tendance à déminuer donc devenir décroissante.

J'ai l'impression que je résonne à l'inverse.

Effectivement, tu ne regardes pas ce qu'il faut...

C'est le SIGNE de -t+5 (qui te donne le SIGNE de s'(t)) qu'il faut regarder

Si tu observes correctement, il n'y a pas de difficulté.

Pour t > 5, -t+5 < 0 , s'(t) < 0 donc s décroissante.

Pour t < 5, -t+5 > 0 , s'(t) > 0 donc s croissante.

Merci beaucoup MTSCHOON, c'est beaucoup plus clair.
Je vais m'entraîner pendant les vacances.

Passer de très belles fêtes.

Complément :

Le maximum est pour t=5

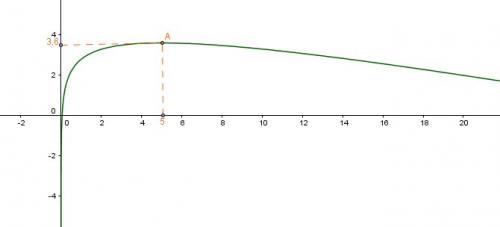
$s(5)=−55+3+ln(5)=−1+3+ln(5)=2+ln(5)s(5)=-\frac{5}{5}+3+ln(5)=-1+3+ln(5)=2+ln(5)$

A la calculette $\approx 3.6$

Je te mets le graphique correspondant à la fonction.

$fichier math$

Je te conseille de refaire seul, tranquillement, en réfléchissant, les exercices relatifs aux variations de fonction que tu as fait.
La logique est toujours la même.
Approfondis et tout s'éclairera.
Ce n'est pas la quantité qui compte, c'est la qualité.

Bonnes vacances à toi et bonnes fêtes.

Bonjour à tous,
je m'entraine sur ce style d'exercice car je ne me sens pas encore assez confiant dessus.

pour s(t)= -t/5 + 4 +ln(t)
je cherche la dérivée:
s'(t)= -1/5 + 1/t =-t/5t + 5/5t= 5-t/5t
j'analyse les variations:

-t+5<0 <=> -t<-5 <=> t>5 (décroissante)
-t+5>0 <=> -t>-5 <=> t<5 (croissante)
la fonction est croissante puis décroissante elle atteint un maximum en 5.

cela est-il juste?

bon après midi

C'est bon.

Merci beaucoup MTSCHOON.

De rien ( et Bonne Année,* je crois que j'ai oublié de te le dire dans mon précédent message*)