Fonction opposée et valeur absolue d'un polynome

Bonjours j'ai un exercice a résoudre mais je n'y arrive pas
La consigne est: On appelle la fonction opposée de f la fonction notée (-f) défini sur I par: (-f)(x)=-f(x).
On appelle Cf la courbe représentation d'une fonction f dans un repère orthonormé (O,I,J)
On considère un point M quelconque de Cf de coordonnées (x;f(x)). On me demande par quelle transformation géométrique obtient on le point M'(x;-f(x)). Pour ma part je pense que c'est une symétrie centrale mais j'en doute par conséquent je suis bloqué lorsque l'on me demande d'en déduire la méthode pour obtenir la courbe représentative de la fonction (-f) à partir de celle de f

Merci d'avance pour votre réponse

Bonjour,

Piste,

Soit M(x f(x) ) un point quelconque de (C), courbe représentative de f

Soit M'(x,-f(x) ) un point quelconque de (C'), courbe représentative de -f

M et M' ont même abscisse et des ordonnées opposées.

M et M' son donc symétriques par rapport à ..................

Je pense que c'est par rapport a l'axe des abscisse
Il s'agit donc d'une symétrie axiale et non centrale je m'étais trompé
est ce bien cela ?

oui, c'est bien ça.

merci beaucoup.
Il m'est ensuite demandé d'en déduire la méthode pour obtenir la courbe représentative de la fonction (-f) à partir de celle de f. Pour répondre à cette question, j'ai justifié en disant que pour représenter (-f), il suffisait simplement de faire la symétrie de f par rapport à l'axe des abscisses. est ce suffisant?
Merci encore

Oui ; c'est la conséquence directe de ce qui est demandé avant.

Super ! Merci beaucoup j'ai bien compris
Cependant je me retrouve embetté une fois de plus dans la seconde partie où on a introduit la valeur absolue avec une fonction polynôme du second degré.
En effet, l'énoncé est le suivant:
on considère la fonction f défini sur R par : f(x) = lx²-2xl
Et on me demande de dresser le tableau de variation de la fonction g(x)= x²-2x.
J'ai trouvé que:

sur l'intervalle ]-∞;1[, la fonction g est décroissante
sur l'intervalle ]1;+∞[, la fonction g est croissante

Est ce correct?

Merci d'avance

Oui, c'est correct.

Le minimum est pour x=1 et g(1)=-1

très bien merci !

ensuite, il m'est demandé de déterminer le signe de x²-2x suivant les valeurs de x dans R
du coup j'ai fais un tableau de signes et je trouve que sur l’intervalle ]-∞;0] c'est positif, sur [0;2] c'est négatif et sur [2;+∞[ c'est positif

est ce correct ?
Merci d'avance

Tout à fait correct (et j'imagine qu'ensuite ton énoncé te demande de donner les expressions de f(x) suivant x)

Pas tout a fais on me demande sa démontrer que si x ∈ ]-∞;0]∪[2;+∞] on a f(x)=g(x) et que si x∈[0;2] on a f(x)=-g(x)

c'est la que cela se complique, je ne comprend pas par ou commencer ?

Et si...ou presque...

Je t'indique le principe relatif aux valeurs absolues

Pour a ≥ 0, |a|=a
Pour a ≤0, |a|=-a

Alors,

Pour x ∈ ]-∞;0]∪[2;+∞[ , g(x) ≥ 0, donc f(x)=....

Pour x ∈ [0,2] , g(x) ≤ 0 , donc f(x)=....

De mon coté j'ai fais :

Si x<0 alors f(x)=lx²-2xl=x²+2x
Si 0<x<2 alors f(x)=lx²-2xl=x²-2x
Si x>2 alors f(x)=lx²-2xl=-x²-2x

est ce correct ?

Non, tes réponses ne sont pas bonnes.

Revois ce que je t'ai indiqué précédemment :

Pour a ≥ 0, |a|=a
Pour a ≤0, |a|=-a

Des exemples pour comprendre
a=3 donc a > 0 |3|=3
a=-3 donc a < 0 |-3|=-(-3)=3
pour a=0, les deux transformations sont bonnes car |0|=0=-0

Si x≤0, vu que g(x) est positif, f(x)=lx²-2xl=g(x)=x²-2x

Si 0≤x≤2, vu que g(x) est négatif, f(x)=lx²-2xl=-g(x)=-(x²-2x)=-x²+2x

Si x≥2, vu que g(x) est positif, f(x)=lx²-2xl=g(x)=x²-2x

Bien sûr , tu peux regrouper le 1er et le 3ème cas, comme te le demande l'énoncé:

**Pour x ∈ ]-∞;0]∪[2;+∞[ ,
g(x) ≥ 0, donc f(x)=g(x)

Pour x ∈ [0,2] ,
g(x) ≤ 0, donc f(x)=-g(x)**

Pour téclairer, je te joins le graphique de g et de f

la représentation graphique de g est la parabole tracée en vert
la représentation graphique de f, tracée en rouge, s'en déduit :

Pour x ∈ ]-∞;0]∪[2;+∞[ , g(x) ≥ 0, donc f(x)=g(x) portions de courbes (vert et rouge) confondues
Pour x ∈ [0,2] , g(x) ≤ 0 , donc f(x)=-g(x) (portions de courbes (vert et rouge) symétriques (voir la symétrie trouvée précédemment)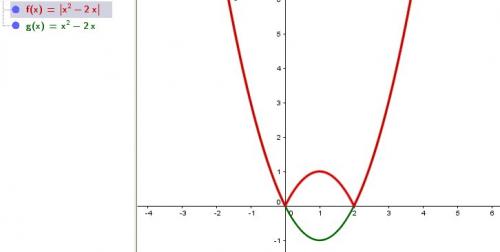

$fichier math$

merci beaucoup je suis désolé de vous répondre maintenant à cause des fêtes de noël
je vous remercie vraiment pour votre investissement
passez de bonnes fêtes de fin d'année

De rien !

Bonnes fêtes à toi !