Déterminer quand des limites ont une forme indéterminée
-
Ddut dernière édition par Hind
Bonjour.
j'ai beaucoup d'exercices sur les limites mais je ne sais pas comment faire.On me demande quand les limites ont une forme indéterminée
comment dois-je procéder?
-
mtschoon dernière édition par

Bonjour,
Il n' a pas de "recette miracle"...
Toute dépend de l'indétermination ...
Donne des exemples précis si tu as besoin d'aide.
-
Ddut dernière édition par
lim t-> -∞
Je dois dire lesquelles on une forme indéterminée.
(e^-8t)/7t: 0+/-∞ = Déterminée
arctan(2t)/exp(8t): -pi/2)/-pi = Déterminée
exp(2t) -4t^2: 0+∞= Déterminée
e^-4t/2t^-7: 0/-∞ =Déterminée
3te^9t: je ne sais pas faire
4/t^9 arctan(9t): arctan=-pi/2 = Déterminée
t^-3 + 6/t: je ne sais pas faire
t^7/2 arctan(8t): arctan=-pi/2 = Déterminée
Pour l'instant je n'ai trouvé aucune limites indéterminée, il y a un problème!
-
mtschoon dernière édition par

Des problèmes, il n'y en a pas qu'un...
Ce serait bien de commencer à indiquer la liste des "formes indéterminées" dont tu parles ton cours.
Il y a 8 fonctions ! ça fait beaucoup pour une seule discussion...
Je regardeta première réponse
Il s'agit, je pense, de la fonction e−8t7t\frac{e^{-8t}}{7t}7te−8t
Si c'est bien ça, lorsque t tend vers -∞, commence par revoir la limite de e−8te^{-8t}e−8t :
Lorsque t tend vers -∞, -8t tend vers .... , e−8te^{-8t}e−8t tend vers ...
-
Ddut dernière édition par
Il y a 0/0; ∞/∞; ∞-∞; 0^0; ∞^0 et 1^∞
mais e^-8*∞ donne quoi comment puis-je le trouver?
-
mtschoon dernière édition par

Merci pour la liste.
∞ n'est pas un nombre. Tu ne peux pas "calculer" avec ∞
(Revois les explications de ton professeur)Raisonne avec logique, en répondant à ma précédente question :
Lorsque t tend vers -∞, -8t tend vers ..... , e−8te^{-8t}e−8t tend vers .....
-
Ddut dernière édition par
-8 tend vers ∞ par contre e^-8t je ne sais pas quelle variation provoque exponentielle
-
mtschoon dernière édition par

Lorsque t tend vers -∞, -8t tend vers +∞, e−8te^{-8t}e−8t tend vers +∞ (c'est une propriété de la fonction exponentielle)
7t tend vers -∞
Donc forme indéterminée
-
Ddut dernière édition par
Donc +∞/-∞ est égal à ∞/∞?
Bonne soirée
-
mtschoon dernière édition par

Pour ta dernière question sur la première fonction : Non, vu que les signes sont différents, mais se sont des indéterminations du même type "∞/∞"
Je regarde ta réponse pourla seconde fonction.
Si j'ai bien lu, il s'agit de arctan(2t)exp(8t)\frac{arctan(2t)}{exp(8t)}exp(8t)arctan(2t), lorsque t tend vers -∞
La forme est bien "déterminée" mais la limite du dénominateur est fausse.
Revois la fonction exponentielle
t tend vers-∞ donc 8t tend vers.......... donc exp(8t) tend vers................
-
Ddut dernière édition par
Merci,
lim t-> -∞
arctan(2t)/exp(8t): -pi/2)/0 Déterminée
exp(2t) -4t^2: 0+∞= Déterminée
e^-4t/2t^-7: 0/-∞ =Déterminée
4/t^9 arctan(9t): arctan=-pi/2 = Déterminée
t^7/2 arctan(8t): arctan=-pi/2 = Déterminée
J'ai vérifié je retrouve les mêmes résultats
-
mtschoon dernière édition par

Précédemment, tu as écrit :
Citation
arctan(2t)/exp(8t): -pi/2)/-pi = DéterminéeLe dénominateur est faux mais je vois que tu l'as rectifié vu que dans ton dernier message tu as mis 0, ce qui est exact.
Je passe à latroisième fonction.
exp(2t)−4t2exp(2t) - 4t^2exp(2t)−4t2
C'est bien "Déterminée" la réponse, mais je vois une faute
Lorsque t tend vers -∞, 4t² tend vers ............, donc -4t² tend vers .............
Merci de rectifier ton erreur
Remarque : je regarde une fonction que lorsque la précédente est traitée correctement.
-
Ddut dernière édition par
Pour -4t^2 je regarde la fonction x^n avec la limite -∞ il a marqué si n est pair (ce qui est le cas car 2 est pair) la limite est : +∞.
Je pense que l'erreur vient de là :
0+ (-∞)= 0-∞ donc fonction déterminée
-
mtschoon dernière édition par

C'est bon pour la troisième fonction.
Je passe à la quatrième fonction.
e−4t2t−7\frac{e^{-4t}}{2t^{-7}}2t−7e−4t ?
e−4t(2t)−7\frac{e^{-4t}}{(2t)^{-7}}(2t)−7e−4t ?
Comme tu écriture n'est pas précise, j'ignore, si, au dénominateur c'est t ou 2t qui est à la puissance -7
Merci de le préciser.
-
Ddut dernière édition par
Il s'agit de la première proposition
-
mtschoon dernière édition par

D'accord.
La réponse est bien "Déterminée", mais il y a une erreur au numérateur.
t tend ver -∞ donc -4t tend vers ...., donc e−4te^{-4t}e−4t tend vers ............
-
Ddut dernière édition par
Dans mon tableau il a marqué que pour exp(x) limite en -∞: il y a marqué 0+
-
mtschoon dernière édition par

Qui te parle de 0+ ?
Je te suggère de connaitre la fonction exponentielle et de raisonner avec logique.
Je repose la question
Complète :
t tend ver -∞ donc -4t tend vers ...., donc e−4te^{-4t}e−4t tend vers ............
-
Ddut dernière édition par
Je bloque sur ça.
-4t n'est pas une constante de ce fait je n'ai aucune fonction de référence dans mon tableau.Peut être que tout simplement:
t tend vers -∞ donc -4t tend vers -∞, donc e-4t tend vers -∞
-
mtschoon dernière édition par

Cette façon de regarder un"tableau" ne me semble pas satisfaite...auras-tu ce "tableau" en devoir surveillé ?
En plus, ce serait mieux de connaitre les fonctions de référence et de raisonner avec du bon sens.
Ceci n'est qu'une opinion personnelle...Tu ne comprends pas que si t tend vers -∞ , en multipliant par -4 (qui est négatif) , le produit -4t tend vers +∞ ? donc e−4te^{-4t }e−4ttend vers +∞ ?
-
Ddut dernière édition par
Car - par - fait plus, ça je suis d'accord.
4t tend vers ∞ mais le fait de rajouter exp après cela ne change rien?
-
mtschoon dernière édition par

Il serait bon que tu connaisses la fonction exponentielle . C'est une fonction de référence. Tu peux éventuellement regarder la courbe sur ta calculette
Regarde.
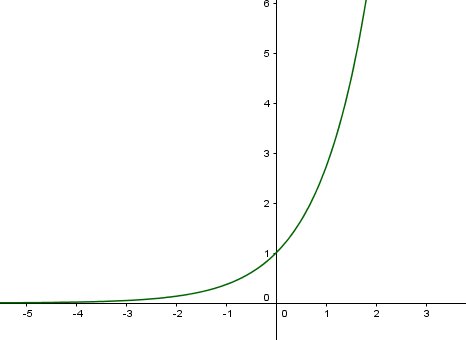
Lorsque l'abscisse augmente indéfiniment ( tend vers +∞), l'ordonnée augmente indéfiniment (tend vers +∞)très très très vite.
exemples
e5e^5e5 ≈148
e10e^{10}e10≈22000
e100e^{100}e100≈2.7x10437x10^{43}7x1043
etc
-
Ddut dernière édition par
Si e^-4t = +∞
Et 2t^-7 =-∞
Cela fait +∞/-∞ ce qui est indéterminée alors que nous avons dit que tout a l'heure la fonction est déterminée
-
mtschoon dernière édition par

Je regarde la cinquième fonction
3te9t3te^{9t}3te9t
(Je suppose que c'est t qui est à la puissance 9t)
Lorsque t tend vers -∞, en multipliant par 3 qui est positif,
3t tend vers -∞
Lorsque t tend vers -∞, en multipliant par 9 qui est positif,
9t tend vers -∞Regarde la courbe de la fonction exponentielle.
Pour des abscisses de valeurs négatives tendant vers -∞, les ordonnées s'approchent très rapidement de 0 ( par valeurs positives)
Donc,e9te^{9t}e9t tend vers 0(on peut préciser 0+, si tu connais, sinon, ne précise pas)
On obtient une forme indéterminée du TYPE "0.∞"
Il y a un problème avec la liste des formes indéterminées que tu as donnée, car cette forme n'y figure pas.
L'as-tu oubliée ?
-
mtschoon dernière édition par

Regarde ici pour la liste complète des formes indéterminées usuelles.
-
Ddut dernière édition par
Je ne l'avais pas.
Pour cet exemple j'ai compris.Par contre j'ai toujours une interrogation pour e^-4t/2t^-7 si j'ai bien compris cela fait +∞/-∞: forme qui est inderminee
-
mtschoon dernière édition par

Lorsque t tend vers -∞, 2t−72t^{-7}2t−7 tend vers 0
Explication : 2t−7=2t72t^{-7}=\frac{2}{t^7}2t−7=t72
Lorsque t tend vers -∞, t7t^7t7 tend vers -∞ et le quotient 2/t72/t^72/t7 tend vers 0, c'est à dire 2t−72t^{-7}2t−7 tend vers 0
Remarque ;: une autre fois, ne mets pas 8 fonctions dans le même topic car, comme tu a des difficultés à chaque fonction, c'est trop long et on ne s'y reconnait plus.
-
mtschoon dernière édition par

Je passe à la sixième fonction.
Est-ce 4t9arctan(9t)\frac{4}{t^9arctan(9t)}t9arctan(9t)4 ?
ou
4t9arctan(9t)\frac{4}{t^9}arctan(9t)t94arctan(9t) ?
-
Ddut dernière édition par
Vous avez raison il sera plus simple, la prochaine fois, que j'essaie de faire l'exercice progressivement, néanmoins j'ai peur de ne pas arriver à terminer le DM pour lundi et par la même occasion de ne pas comprendre.
Il s'agit de la deuxième proposition.
4/t^9 tend vers -∞
Arc tan (9t) tend aussi vers -∞
-∞*-∞= -∞ donc fonction déterminée
-
mtschoon dernière édition par

C'est donc la seconde écriture
(Si tu mettais des parenthèses, ça fera gagner du temps...)
Pour la sixième fonction, il s'agit bien d'une forme "déterminée", mais tes réponses sont mauvaises.
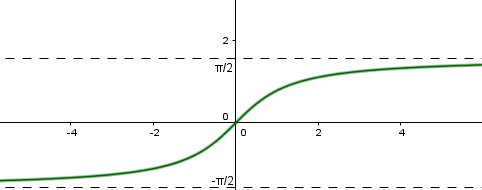
Lorsque t tend vers -∞, t9t^9t9 tend vers -∞, donc 4/t94/t^94/t9 tend vers 0
Lorsque t tend vers -∞, t9t^9t9 tend vers -∞, donc arctan(9t) tend vers -∏/2
Je te joins la courbe de arctan : c'est une fonction de référence à connaître.
-
mtschoon dernière édition par

Je passe à la septieme fonction
Encore une ambiguïté
est-ce
t−3+6t ou t−3+6tt^{-3}+\frac{6}{t} \ ou \ \frac{t^{-3}+6}{t}t−3+t6 ou tt−3+6 ?
-
Ddut dernière édition par
Je n'arrive pas à me représenter que 4/-∞ puisse faire quasi 0, dans mon raisonnement je me dit je divise 4par l'infini cela me fait l'infini. Dans ce cas il me semble que c'est un problème de représentation.
Il s'agit de la première
-
mtschoon dernière édition par

Allons-y pour la première écriture.
ttt^{-3}=1/t3=1/t^3=1/t3
Lorsque t tend vers -∞, t3t^3t3 tend vers -∞ donc 1/t31/t^31/t3 tend vers 0 donc t−3t^{-3}t−3 tend vers 0
Lorsque t tend vers -∞, 1/t tend vers 0
La somme tend vers 0+0=0
Forme déterminée.
Merci de re-écrire la huitième fonction avec des parenthèses (si tu n'utilises pas le LaTex)
-
mtschoon dernière édition par

Nos réponses se sont croisées.
Pour comprendre "4/-∞"
Il s'agit je suppose de 4/t94/t^94/t9
Dire que t9t^9t9 tend vers -∞ veut dire que t9t^9t9 prend des valeurs négatives et de plus en plus grandes en valeurs absolues :
exemples :
-10, -100, -1000, etc
4/(-10)=-0.4
4/(-100)=-0.04
4/(-1000)=-0.004
etc
Le quotient tend vers 0 (ici par valeurs négatives)
-
Ddut dernière édition par
Merci Mtschoon pour l'explication c'est enfin clair.
Pour (t^7/2) arctan(8t)
Lorsque t tend vers -∞, t^7 tend vers -∞, donc t^7/2 tend vers -∞
Lorsque t tend vers -∞, arctan(8t) tend vers -∏/2
La fonction est déterminée.
-
mtschoon dernière édition par

OUI !
La dernière est juste.
(Précise que Lorsque t tend vers -∞, 8t tend vers -∞, arctan(8t) tend vers -∏/2)
-
Ddut dernière édition par
POUR T -> +∞
e^7t/6t^5Lorsque t tend vers +∞, 7t tend vers +∞; donc 7t tend vers +∞
Lorsque t tend vers +∞, 6t tend vers +∞; donc 6t^5 tend vers +∞
Donc, e^7t tend vers 0+
On obtient une forme déterminée du TYPE "0/+∞"
-
mtschoon dernière édition par

Encore une ?
Si tu en as d'autre(s), ouvre un autre topic**, merci.**
A revoir !
Lorsque t tend vers +∞, 7t tend vers +∞; donc e7te^{7t }e7ttend vers +∞
J'ignore si c'est 6t ou seulement t qui est à la puissance 5, mais ça ne change pas le résultat.
Lorsque t tend vers +∞, 6t^5 tend vers +∞
On obtient une forme indéterminée du TYPE "∞/∞"
-
Ddut dernière édition par
∞/∞ fait partie des 7 formes indéterminées.
Pourquoi s'agit t-il d'une forme déterminée?
-
mtschoon dernière édition par

C'est exact . Forme indéterminée.