Limites/Indétermations2
-
Ddut dernière édition par
Bonsoir,
t -> +∞
exp(5t) -t^6= +∞ - (+∞) = +∞-∞ FORME DETERMINEE
ln(9t) - 4√t= +∞ -(+∞) = +∞-∞ FORME DETERMINEE
(ln(6t))/5√t= +∞/+∞= FORME INDETERMINEE
-
mtschoon dernière édition par

Bonsoir,
Attention,
Dans ces 3 cas, la forme est INDETERMINEE (∞-∞ , ∞/∞)
-
Ddut dernière édition par
Je suis désole, j'en ai encore beaucoup mais je crois que je suis en train de comprendre.
pour:
9t^7 -ln(2t)= +∞ -∞ INDETERMINEE
e^8t - 6e^-7t= +∞ -(-∞) DETERMINEE
7t^9 -7/t= +∞-0 DETERMINEE
7t^2 +3t^4= ∞+∞ INDETERMINEE
-
mtschoon dernière édition par

Il y a une erreur pour celle-là :
Citation
e^8t - 6e^-7t= +∞ -(-∞) DETERMINEELorsque t tend vers +∞, -7t tend vers -∞, e−7te^{-7t}e−7t tend vers 0
(regarde la courbe de la fonction exponentielle que je t'ai donnée dans l'autre topic)Les 3 autres sont bonnes.
-
Ddut dernière édition par
Bonjour,
Comment dois faire pour:
T-> +∞(8/t)^(9t)
Quand j'essaie de le faire je trouve 0*+∞ ce qui serait une forme indéterminée.
-
mtschoon dernière édition par

Si j'ai bien compris, pour l'instant, tu ne calcules pas les limites. Tu dois seulement indiquer s'il s'agit d'une forme indéterminée ou non.
Ici, 8/t tend vers 0
9t tend vers +∞Regarde la liste des formes indéterminées.
Cette forme n'en fait pas partie.
Elle est "déterminée"
-
Ddut dernière édition par
Bonjour Mtschonn,
Tout-à-fait nous avons des expressions et nous devons dire si elles sont indéterminées.
Pour le précédent j'ai fait une faute de frappe, pour moi il s'agit de 0*∞ qui est une forme indéterminée.
-
mtschoon dernière édition par

Est-ce
(8t)9t\ (\frac{8}{t})^{9t} (t8)9t
C'est à dire (8/t) à la puissance (9t) ?
Si c'est bien ça (qui correspond à ce que tu as écrit), relis ma réponse .
Sinon, re-écrit la fonction correctement.
-
Ddut dernière édition par
Non c'est bien la proposition que vous donnez.
Je relis votre reponse, néanmoins c'est équivalent à (8/t) *^(9/t)
-
mtschoon dernière édition par

Mais..., pourquoi mets-tu un signe de multiplication (*) ? ? ?
Il n'y a pas de multiplication, vu qu'il s'git d'une puissance.
Symboliquement, la forme est " 0∞0^\infty0∞"
Je te remets le lien sur les formes indéterminées usuelles
-
Ddut dernière édition par
Merci Mtschoon, je me représentais la puissance en multiplication ce qui est absurde.
-
Ddut dernière édition par
Pour les prochains je vais les faire tout seul.
Vous n'aurez qu'à me dire qu'elles expressions comportent des erreurs, j'essayerai de les corriger moi même, je ne veux pas vous embêter trop.T-> +∞
6t^5 -5/t = +∞-0 DÉTERMINÉE
5te^-9t= +∞^-∞ DÉTERMINÉE
sin(9t)/5= +∞/+∞ INDÉTERMINÉE
-
mtschoon dernière édition par

Je regarde.
Le premier écrit est bon
le second est mauvais (si c'est bien 5t.e−9t5t.e^{-9t}5t.e−9t) , car e−9te^{-9t}e−9t ne tend pas vers -∞
Je t'ai donné la courbe de la fonction exponentielle mais je constate que ça ne sert à rien !
Pour la troisième, il s'agit peut-être de sin(9t)5\frac{sin(9t)}{5}5sin(9t)
L'explication ne peut pas être bonne car un sinus prend des valeurs comprises entre -1 et +1
Voici la courbe de la fonction sinus
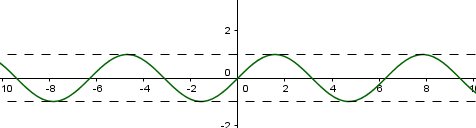
-
Ddut dernière édition par
Pour le premier exponentielle tend vers 0 donc +∞^0 INDÉTERMINÉE
Pour le deuxième: (sin(9t))/5t = pas de limites/ +∞ ce qui fait DETERMINEE
-
mtschoon dernière édition par

Je suppose que le "premier" dont tu parles le "premier faux".
cette fois, c'est bon
Je vois que le "second faux" a changé d'expression. Il y a maintenant 5t au dénominateur... ! ! !
c'est bon.
-
Ddut dernière édition par
Pour t-> +∞
(e^-3t)/(9t^-2) = -∞/-∞ DÉTERMINÉ
(e^-8t)/9t= -∞/∞ DÉTERMINE
4arctan(t) ln(5t) = pi/2*+∞ DÉTERMINÉ
(Arctan(6t))/exp(8t) = pi/2/+∞ DÉTERMINÉ
Le fait que aucune soit indéterminée me gêne car généralement il y en a au moins une.
-
mtschoon dernière édition par

Ma patience ayant des limites, lorsque je voies encore écrit que e−3te^{-3t }e−3t et e−8te^{-8t}e−8t tend vers -∞, je ne supporte plus.
Il faudrait que les conseils donnés servent à quelques chose !
-
Ddut dernière édition par
Après rectification:
(e^-3t)/(9t^-2) = 0/-∞ DÉTERMINÉ
(e^-8t)/9t= 0/∞ DÉTERMINE
4arctan(t) ln(5t) = pi/2*+∞ DÉTERMINÉ
(Arctan(6t))/exp(8t) = pi/2/+∞ DÉTERMINÉ
-
mtschoon dernière édition par

Le 1er est faux à cause de 9t−29t^{-2}9t−2 (principe expliqué précédemment)
Le reste va.
-
Ddut dernière édition par
Je risque de me faire souffler dans les bronches mais j'ai repris les anciens messages et quand je fais le calcul:
e^-3t = 09*t =+∞
+∞^-2 = -∞
-
mtschoon dernière édition par

RAPPEL
(9t)−2=1(9t)2(9t)^{-2}=\frac{1}{(9t)^2}(9t)−2=(9t)21
t tend vers +∞ donc (9t)² tend vers +∞ donc 1/(9t)² tend vers 0 donc (9t)−2(9t)^{-2}(9t)−2 tend vers 0
-
Ddut dernière édition par
c'est une notion que je n'avais pas complétement acquise. je l'ai intégré dans ma fiche de révision.
La forme est déterminée.
-
Ddut dernière édition par
Je vous embête encore pour 4 formes, je ferai les autres seul, j'ai suffisamment d'exemples.
t -∞
t^9 exp(5t) = -∞*0 DETERMINEE
exp(5t)/t^5 = 0/+∞ DETERMINEE
sin(6t)/8t = pas de limites/-∞ DETERMINEE
(1+(8/t)) ^t = 8/t tend vers 0 ; 0+1 =1; 1^-∞ DETERMINE
-
mtschoon dernière édition par

Citation
je ferai les autres seulBonne idée !Une erreur à la seconde fonction à cause de t5t^5t5 ( il y a 5 facteurs égaux à t, donc...)
Pour la dernière, c'est de la FORME "1∞1^∞1∞" donc c'est une forme indéterminée (malgré le "-")
Le reste est bon.
-
Ddut dernière édition par
exp(5t)/t^5 = 0/0 INDÉTERMINÉE
Donc 1^-∞ est égal à 1^∞
-
mtschoon dernière édition par

Attention : Lorsque t tend vers -∞, t5t^{5 }t5tend vers -∞
exp(5t)/t5exp(5t)/t^5exp(5t)/t5 de la forme 0/-∞ "Déterminée"
Pour les formes indéterminées, "égal" ne veut rien dire...
C'est du même type ( c'est symbolique 1∞1^∞1∞ symbolise "1+∞1^{+∞}1+∞" et "1−∞1^{-∞}1−∞")
-
Ddut dernière édition par
Merci Mtschoon de m'avoir aidé tout au long de ce travail bonne soirée et bonne semaine.