Fonction au carré
-
RRosalie83 dernière édition par
Bonsoir,
Je suis sur la résolution d'un exercice d'un Devoir Maison, j'ai commencé la résloution et je me demande si je suis sur la bonne voie.
Exercice:
Soit f la fonction définie sur R{-2} par:
f(x) = -3/(x+2)²+1
Question: Montrer que f est décroissante sur ]-∞;-2[ grâce à l'étude du signe de f(a)-f(b)
Difficulté: Avec cette méthode, je n'arrive pas à établir le tableau des signes.
Résolution en cours:
1/ Démonstration:
On calcule f(a)-f(b) = -3/(a+2)² +1 - (-3/(b+2)² +1)
= -3/(a+2)² +1 +3/(b+2)² -1
= -3/(a+2)² +3/(b+2)²
= -3 (b+2)²/ (a+2)(b+2)² + 3(a+2)²/(b+2)²(a+2)²
= -3(b² +4b+4)/ (a+2)²*(b+2)² + 3(a²+4a+4)/(b+2)²*(a+2)²
= -3b²-12b-12/ (a+2)²*(b+2)² +3a² +12a+12/(a+2)²*(b+2)²
= -3b²-12b+3a²+12a/ (a+2)²*(b+2)²
= b (-3b-12)+a(3a+12)/ (a+2)²*(b+2)²
Tableau de signes: Avec ce calcul, je n'arrives pas a établir le tableau de signes pour démontrer quelle est décroissante.
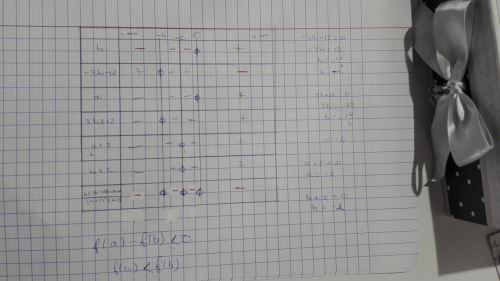
En vous remerciant d'avance pour m'aider à trouver la voie de cette résolution.
Rosalie83
-
mtschoon dernière édition par

Bonjour,
Je suppose qu'il s'agit bien de f(x)=−3(x+2)2+1f(x)=-\frac{3}{(x+2)^2}+1f(x)=−(x+2)23+1
a < -2 et b < -2
Il faut que tu transformes f(a)-f(b) en factorisant le numérateur
Reprends tes calculs
Tu dois trouver :
f(a)-f(b)=[3(a²-b²+4a-4b)] / [(a+2)²(b+2)²]
Tu factorises le numérateur par (a-b)
Tu dois trouver
f(a)-f(b)= [3(a-b)(a+b+4)] / [(a+2)²(b+2)²]
Sans tableau, tu raisonnes su les signes de chaque facteur.
Si a < b , a-b < 0 . tu dois trouver f(a)-f(b) > 0 d'où f(a) > f(b) d'où
f décroissante sur ]-∞,-2[Désolée pour l'écriture, les codes LaTex et BB se sont bloqués...et j'ai écrit seulement en texte mal lisible...
-
RRosalie83 dernière édition par
Bonsoir,
Je vous remercie pour votre aide et grâce a celle-ci j'ai réussi et compris mon exercice.
Merci encore beaucoup
Rosalie 83
-
mtschoon dernière édition par

De rien !
Bon DM.