fonction polynôme troisième degré

Bonjour,
Ma prof m'a donné, dans un dm, plusieurs exos sur le troisième degré (pas au programme il me semble...), et un seul me pose problème. L'énoncé est:

"La courbe ci-dessous représente sur [-1;2] une fonction polynôme f de degré 3.
Retrouver l'équation de cette courbe".

Malheureusement, impossible de joindre un fichier....
Pour la courbe simple à décrire heureusement, elle commence à un premier point nommé A (-1;2) (semble monter avant mais on ne peut pas savoir...) , puis la courbe descend jusqu'à l'origine (0;0), continue à descendre jusqu'à un point B (1;-2), et remonte brutalement jusqu'à un point C (2;2), après quoi elle semblerait continuer à monter très haut vu la pente qu'elle entame avant C. De plus, deux petites flèches sont tangentes au point B et parallèles à l'axe des abscisses; enfin, une autre petite flèche est tangente au point A et parallèle au même axe.
Encore désolé, je n'avais pas le choix...

Le manque d'informations est donc crucial... J'ai donc commencer par déclarer que le point B est un extremum local (minimum), et j'ai été contraint de conjecturer que le point A est aussi un extremum local (maximum) du fait que la tangente à Cf en ce point semble être parallèle à l'axe des abscisses, et qu'en tant que polynôme de degré 3, si f admet un extremum, elle doit forcément en admettre un second (il me semble qu'elle en admet soit 2 soit zéro comme dans le cas de x->x^3 me semble-t-il), dans le cas contraire je ne voyais pas comment avancer.
Je me suis donc appuyé sur le fait que 0 est une racine évidente, et donc dans ce cas là,
ax^3+bx^2+cx+d = 0 <-> a0+b0+c0+d = 0 <-> d=0. On obtient donc cette équation: ax^3+bx^2+cx = 0.
Ensuite j'ai donc factorisé, ce qui me donne (x-0)(Ax^2+Bx+C). Sauf que voilà, bien que je connaisse des coordonnées de points je ne sais plus où aller x) je suis donc obligé de demander de l'aide, ce que je déteste faire xD
Merci d'avance pour votre aide!!

Bonjour,

Ici, tu es autorisée à scanner ton graphique sans texteet l'ajouter .

Clique sur "Ajoute une image" au dessous du cadre texte.

mtschoon
Bonjour,

Ici, tu es autorisée à scanner ton graphique sans texteet l'ajouter .

Clique sur "Ajoute une image" au dessous du cadre texte.

Justement, il y a eu un problème et ca n'a pas fonctionné. Et je n'ai pas de scanner :frowning2:

Dommage...

Avec ce que tu as écrit ( et ce que j'ai compris) :

$f(x)=ax^3+bx^2+cx+d$

$\left{f(-1)=2 \ f(0)=0 \ f(1)=-2 \ f'(-1)=0 \ f(1)=0\right$

Tu mets donc le problème en équations ce qui te donne un système à résoudre pour trouver a,b,c,d.

D'ailleurs, tu as 5 équations alors que 4 auraient suffit vu qu'il y a 4 inconnues.
Tu résous avec 4 équations et tu vérifie ensuite que la 5ème est bien satisfaite.

Je t'indique ce que tu dois trouver, sauf erreur :
a=1, b=0, c=-3, d=0

$f(x)=x^3-3x$

Bons calculs.

Tiens nous au courant si tu as un problème.

Remarque : cet exercice est tout à fait du programme de 1S car il s'agit d'une fonction polynôme ( et non d'une équation du 3ème degré à résoudre)

Je suppose que ta courbe, sur [-1,2], ressemble à ça, avec, en plus les tangentes horizontales en A et en B

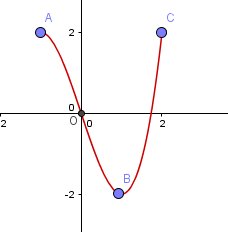
$fichier math$

Merci beaucoup pour ta réponse, je vais essayer
En effet il se peut que ce soit du niveau 1S, c'est juste le manque d'infos au premier coup d'oeil qui m'a fait penser ca x)
Sinon exact la courbe est comme ca, merci

De rien !

Reviens si tu n'y arrives pas.

En effet, en faisant un p'tit système et en s'aidant de la dérivée c'est vite trouvé, merci faudrait que je prête plus d'attention aux éléments que l'on me donne plutôt que d'aller chercher à l'autre bout de la terre... :rolling_eyes:

C'est toi qui a fait les calculs !

C'est bien.

Bon DM.

A+