Analyse de fonction exponentielle

[itsvlnt2]

Bonjour, je dois bientôt rendre un devoir pour le cours de mathématique, il s'agit de réaliser une analyse complète de la fonction $e^{1/lnx}$
seulement, lorsque j'essaie de déterminer les limites de celles-ci afin de trouver les asymptotes, je me perd et ça me bloque.

J'espère que vous pourrez m'aider, je vous remercie d'avance !

Je vous laisse ici le début de mon analyse :

$F(x)=e^{1/lnx}$
Dom f(x)= ℝ
Im f(x)= ℝ$$^+$_0$
zéros: f(x) = 0
$e^{1/lnx}$ =0 IMP car e ≠ 0
pas de zéros
Intersections avec les axes
∩0x = $e^{1/lnx}$= 0 IMP
PAS D'INTERSECTION AVEC L'axe x
∩0y = $e^{1/ln0}$
ln0 ∃
PAS D'INTERSECTION avec L'axe y
Paritéf(x)≠f(-x) pas paire
f(-x) ≠ -f(x) pas impaire
Signela fonction est strictement positive

[mtschoon]

Bonjour,

Je crois voir des erreurs...

Dès le début :

conditions d'existence :

x >0 pour que lnx existe

lnx ≠0 c'est à direx ≠...., pour que 1/lnx existe

Revoir cela et donne le bon ensemble de définition.

[itsvlnt2]

Bonjour, effectivement oui le domaine est ]0;1[U]1;+oo[
Mais je ne trouve pas les asymptotes, le signe de la fonction et la croissance de la fonction

[mtschoon]

Pour que tu puisses vérifier tes réponses, je commence par te donner le graphique.
La courbe est en bleu
Les asymptotes sont en rouge
Les points A et B (en rouge) n'appartiennent pas la la courbe. Ils sont obtenus par "limites".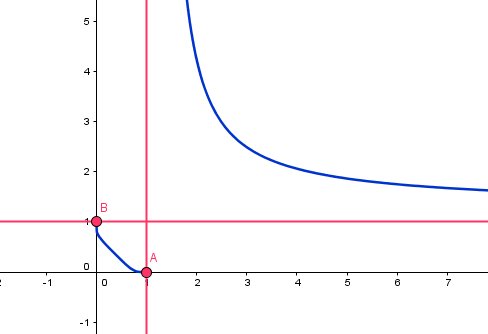

Je regarderai tes réponses dès que possible.

[mtschoon]

Ton domaine rectifié est bon.

Je te détaille un peu limites et asymptotes.

Lorsque x tend vers $0^{+}$, lnx tend vers -∞, 1/lnx tend vers 0 donc f(x) tend vers $e^0$=1 (point B, qui ne fait pas partie de la courbe)

Lorsque x tend vers $1^{-}$, lnx tend vers $0^{-}$, 1/lnx tend vers -∞, donc f(x) tend vers 0 (point A, qui ne fait pas partie de la courbe)

Lorsque x tend vers $1^{+}$, lnx tend vers $0^{+}$, 1/lnx tend vers +∞, donc f(x) tend +∞ (Asymptote d'équation x=1)
Lorsque x tend vers +∞, lnx tend vers +∞, 1/lnx tend vers 0, donc f(x) tend vers $e^0$=1 (Asymptote d'équation y=1)

Pour le signe de f(x) est les intersections de la courbe avec les axes, c'est "évident".

Pour le sens de variation, tu dois calculer la dérivée de f

f est de la forme $e^U$, U est une fonction de x

La dérivée est U'.$e^U$

Donne nous tes calculs si tu as besoin d'une vérification.