Integrales impropres
-
Ddut dernière édition par
Bonjour,
Nous avons commencé la semaine dernières les intégrales impropres. sujet où je n'ai rien compris.Après plusieurs recherches sur internet pour ∫0+∞exp(−6t)dt\int_{0}^{+\infty}{exp(-6t)dt}∫0+∞exp(−6t)dt
j'ai trouvé 1/6Mais pour des formes comme ∫−49λ(11t)dt\int_{-4}^{9}{\lambda(11t)dt}∫−49λ(11t)dt je ne sais pas quoi faire.
je pense à la réponse 0 car les bornes indiquées ne sont pas impropres.
-
mtschoon dernière édition par

Bonsoir,
C'est bon pour la première.
Pour la seconde, j'ignore ce que représente cette fonction "Lambda"...
C'est un terme non usuel, peut-être lié à des mathématiques appliquées ? (appliquées à quoi ? aux signaux ?... )
Peut-être peux-tu nous donner la définition de ce λ\lambdaλ
-
Ddut dernière édition par
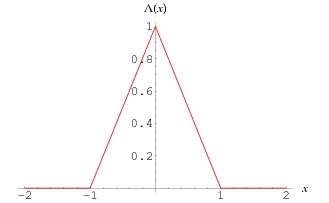
Il s'agit de la fonction triangle.
-
mtschoon dernière édition par

Désolée, mais la fonction "triangle" ? ? ? ...
Il doit y avoir des histoires de signaux la dessous....
Tu peux faire le changement de variable x=11t pour te ramener à λ(x)\lambda(x)λ(x) mais ensuite les bornes sont -44 et 99 et j'ignore la "forme" du schéma dans ce cas...ni la façon que tu as pour faire le calcul.
Personnellement, sans avoir ton cours, je ne peux pas t'aider...
-
Ddut dernière édition par
Oulala je ne sais pas comment je vais m'en sortir. Dans mes exemples je n'ai que avec la fonction exponentielle.
Par contre pour ∫−∞0(1/(3−4)2\int_{-\infty }^{0}{(1/(3-4)^2}∫−∞0(1/(3−4)2 vous pouvez peut être m'aider.
-
mtschoon dernière édition par

Pour ta fonction triangle, ton professeur de donnera forcément une explication. Si tu ne l'as pas, attends qu'il te la donne.
Tu as dû te tromper en écrivant car ta dernière intégrale n'a aucun sens ...il n'y a pas de variable...
-
Ddut dernière édition par
Je reprends:
∫−∞01(3−4t)2dt\int_{-\infty }^{0}{\frac{1}{(3-4t)^2}}dt∫−∞0(3−4t)21dt
-
mtschoon dernière édition par

Je m'interroge sur cette fonction triangle représentée par la tracé en rouge dans ton schéma précédent.
L'intégrale de la fonction "triangle" est l'aire de la surface comprise entre la courbe en rouge et l'axe des abscisses, c'est doncl'aire du triangle central.
Si on se réfère à ton schéma, cette aire vaut 1 ((base fois hauteur)/2)$\bigint _{-1}^{+1}\lambda(x)dx=1$
Regarde si c'est cela qui est écrit dans ton cours.
Ensuite, il faut savoir ce que représente cette fonction triangle entre -44 et +99.Est-ce une suite de triangles identiques?
Dans ce cas, il suffit de compter le nombres de triangles entre ces 2 valeurs.
Ou est-ce toujoursun seul triangle (celui représenté sur le schéma)
Je l'ignore...Regarde ton cours de près et/ou demande à ton professeur, ou attends qu'il donne des explications en classe.
Ce doit être tout simple mais on ne peut pas l'inventer.
Pour ta dernière intégrale :
Utilise les primitives usuelles de ton cours
Une primitive de 1(3−4t)2\frac{1}{(3-4t)^2}(3−4t)21 est 14(13−4t)\frac{1}{4}(\frac{1}{3-4t})41(3−4t1)
Après calculs, tu dois trouver :
$\bigint_{-\infty}^0 \frac{1}{(3-4t)^2}=\frac{1}{12}-0=\frac{1}{12}$
-
Ddut dernière édition par
Merci beaucoup MTSCHOON pour toute votre aide.
Je viens, à l'instant, d'envoyer un mail à mon professeur pour qu'il tente de m'expliquer tout ça.Passer une bonne soirée.