Résoudre un exercice en utilisant les angles orientés

[loulounts]

Bonjour,

J'ai beaucoup de difficultés avec ce DNS : (Merci d'avance).

---

Situation :
A et B sont deux points distincts du plan.
I est le milieu de [AB].
Δ est la médiatrice de [AB].
α est un réel dans [0;π]

Objectif :
Déterminer Eα l'ensemble des points M du plan différents de A et de B tels que :
(MA,MB)=α [2π]

1. Déterminer E0 et En

2. On suppose maintenant que α ∈ ]0;π/2[. On construira une figure, complétée au fur et à mesure.

a) Montrer qu'il existe un unique point O sur Δ tel que (OA,OI)= α [2π]

b) Justifier alors que (OA,OB)= 2α [2π]

c) Soit C le cercle de centre O et passant par A. Montrer que pour tout point P de C, différent de A et B :
(PA,PB) = α [2π] ou (PA,PB) = α + π [2π]

d)Soit M ∈ Eα, c'est-à-dire tel que (MA,MB) = α [2π].
Montrer que M est sur C

e) Conclure : préciser à quoi correspond Eα sur la figure.

3. Tracer sur une figure dans 2 couleurs différentes E π/3 et E π/6. On ne demande pas de justifications.

---

1. Pour E0 :
   (MA,MB) = 0
   Je ne sais pas où on doit placer M.
   M doit être différent de A et B. Si je le place sur [AB], ça ne fonctionne pas, puisque j'aurais (MA,MB) = π.
   Et comme α ∈ [0;π] je ne peux pas le placer en dehors du cercle trigonométrique. Enfin, je pense que non...
   Du coup, je bloque...[texte du lien](url du lien)

[mtschoon]

Bonjour,

Je suppose qu'il s'agit d'angles de vecteurs

Je regarde la 1), pour te permettre d'avancer.

Trace la droite (AB)

$(\overrightarrow{ma},\overrightarrow{mb})=0[2\pi ]$

M est situé sur la droite (AB) à l'extérieur du segment [AB]

$(\overrightarrow{ma},\overrightarrow{mb})=\pi [2\pi ]$

M est situé sur la droite (AB) entre A et B

[loulounts]

Oui, en effet, il s'agit bien d'angles de vecteurs.

Donc pour la 1) : ok. Merci.
Je ne pensais pas qu'on pouvait aller à l'extérieur de [AB].

2)a)
O se place Δ différent de O et de π/2.
Dois-je faire un cercle trigonométrique ?
Et comment démontrer qu'il existe un unique point ? J'en vois une infinité... entre I et le cercle trigonométrique.

[mtschoon]

Bizarre ce que tu écris dans ton énoncé...à la 2
Citation
a) Montrer qu'il existe un unique point O sur ∇ (delta) tel que (OA,OI)= α [2π]

b) Justifier alors que (OA,OB)= α [2π]

Si (OA,OI)= α , alors (OA,OI)= 2α...

Vérifie ton énoncé.

[loulounts]

Oui, pardon.
Pour le b) c'est (OA,OB)= 2α [2π] (j'ai fait la modification dans l'énoncé.)

Pour le b) je pense qu'avec le théorèmes des angles inscrits et au centre ça doit fonctionner.
Mais pour le a), je ne vois vraiment pas où placer le point O...

[mtschoon]

Pour le 2)b), pense à autre chose car dans les questions 1) et 2), il n'y a aucun cercle...

Pour le 2)a), analyse la question

La somme des angles d'un triangle vaut ∏

Le triangle OAI sera rectangle en I ; la somme des 2 angles aigus devra valoir ∏/2

$(\overrightarrow{ai},\overrightarrow{ao})+(\overrightarrow{oa},\overrightarrow{oi})=\frac{\pi }{2}[2\pi ]$

d'où

$(\overrightarrow{ai},\overrightarrow{ao})=\frac{\pi }{2}-\alpha [2\pi ]$

Tu en déduis la construction

Par le point A, tu traces la demi-droite [Az) qui fait un angle de $\frac{\pi }{2}-\alpha$avec la demi-droite [AB)

[Az) coupe Δ en un point unique O

[loulounts]

Bonjour,
(désolé pour mon absence)

Si cela ne vous dérange pas, j'aimerais finir l'exercice. Merci d'avance.

Citation
Le triangle OAI sera rectangle en A

Il n'est pas plutôt rectangle en I ?

pour le b) :

B étant le symétrique de A par rapport à I et comme une symétrie conserve les angles, alors (OI,OB) = (OA,OI)
(OI,OB) + (OA,OI) = (OA,OB)
D'où, (OA,OB) = α + α = 2α [2π]

Pour le c) :

(PA,PB) est un angle inscrit au cercle C interceptant l'arc AB
(OA,OB) est un angle au centre au cercle C interceptant l'arc AB

Or, si un angle inscrit intercepte le même arc de cercle qu'un angle au centre, alors il mesure la moitié de ce dernier.

Donc, (PA,PB) = α [2π]

Pour le d) :

Si deux angles inscrits sont interceptent le même arc de cercle et qu'ils sont égaux, alors leur sommet appartiennent au même cercle.
(Je ne sais pas si ça peut se dire ainsi...)

Comme P ∈ C, alors M ∈ C

Pour le e) :

Eα est le périmètre du cercle de centre O et de rayon [OA]

Pour le 3) :

Il faut que (OA,OI) = 60° (pour l'un) et 30° (pour l'autre) ?

[mtschoon]

Oui, Le triangle OAI sera rectangle en I

Oui pour le b)

Je regarde le c)

Le théorème est bien le bon, mais fait attention aux [2∏]

$\text{(\vec{oa},\vec{ob})=2(\vec{pa},\vec{pb}) \ [2\pi]$

En divisant TOUT par 2

$\text{(\vec{pa},\vec{pb})=\frac{1}{2}(\vec{oa},\vec{ob}) \ [\pi]$

d'où

$\text{(\vec{pa},\vec{pb})=\frac{1}{2}(2\alpha) \ [\pi]$

$\text{(\vec{pa},\vec{pb})=\alpha \ [\pi]$

Cela veut dire :

$\text{(\vec{pa},\vec{pb})=\alpha +k\pi, k\in z$

Il te reste à distinguer le cask pair et le cask impair.

[loulounts]

Si k est pair :
(PA,PB) = α [2π]

Si k est impair :
(PA,PB) = α + π [2π]

[mtschoon]

Oui.

Lorsque $(\overrightarrow{pa},\overrightarrow{pb})=\alpha [2\pi ]$ , le point P est sur le "grand arc" d'extrémités A et B, du cercle (C)

Lorsque $(\overrightarrow{pa},\overrightarrow{pb})=\alpha +\pi [2\pi ]$, le point P est sur le "petit arc" d'extrémités A et B, du cercle (C)

[loulounts]

Ah ok...
Ma logique n'est pas terrible !

Oui, effectivement je comprends mieux le sens du fait que k est pair ou impair. Merci !

Citation
Pour le d) :

Si deux angles inscrits sont interceptent le même arc de cercle et qu'ils sont égaux, alors leur sommet appartiennent au même cercle.
(Je ne sais pas si ça peut se dire ainsi...)

Comme P ∈ C, alors M ∈ C

Pour le e) :

Eα est le périmètre du cercle de centre O et de rayon [OA]

Pour le 3) :

Il faut que (OA,OI) = 60° (pour l'un) et 30° (pour l'autre) ?

La suite est juste ?

[mtschoon]

Non, ton raisonnement au 2) d) n'est pas bon.

Il s'agit de la réciproque de la question précédente.

Par hypothèse :$(\overrightarrow{ma},\overrightarrow{mb})=\alpha [2\pi ]$

Il faut prouver que M est sur (C)

Une piste possible,

Vu que 0 < α < ∏/2, M A B ne sont pas alignés.

Il existe donc un cercle (C') , de centre O' , passant par M A B.

En utilisant la même idée qu'au 2)a) :

Par le point A, tu traces la demi-droite [Az) qui fait un angle de $\frac{\pi }{2}-\alpha$ avec la demi-droite [AB)

[Az) coupe Δ en un point unique O'

Conclusion :O'=O et (C')=(C) donc $m\in (c)$

Une remarque pour ces deux constructions ( celle du 2)a ) et celle du 2)d) )

Il y a une façon qui revient au même et qui est commode (à condition qu'elle soit dans ton cours, ce que j'ignore) : construire la tangente en A au cercle

Si tu connais ce théorème relatif aux angles inscrits :

T étant un de point de la tangente en A au cercle :

$(\overrightarrow{ma},\overrightarrow{mb})=(\overrightarrow{at},\overrightarrow{ab})$

donc

$(\overrightarrow{at},\overrightarrow{ab})=\alpha [2\pi ]$

Tu peux ainsi construire (AT) puis, en traçant la perpendiculaire en A à (AT), obtenir [Az),qui coupe (Δ) au centre du cercle.

Pour le 2)e), ne parle pas de "périmètre" (revois la définition du mot "périmètre")

De plus, revois ce qui a été démontré : (Eα) n'est pas TOUT le cercle.

Pour le 3),tu peux donner le graphique que tu as fait, si tu as besoin d'une vérification.

[mtschoon]

Au cas où..., je te mets la construction de $E_{\prod /3}$ en BLEU sur le graphique.

Regarde de près et lorsque tu as bien compris, tu traces $E_{\prod /6}$ d'une autre couleur.

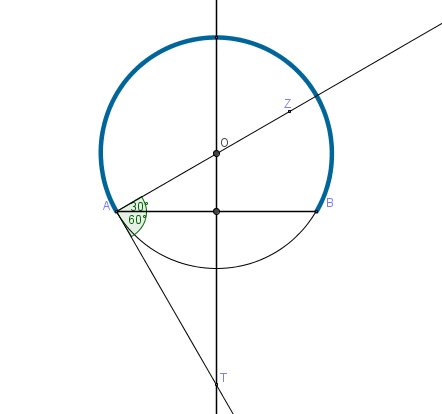
Bonne fin de DM.