Etudier les variations et la dérivabilité d'une fonction avec valeur absolue

[Monopanda]

Bonjour, je n'arrive pas a répondre a la 4 et 5 et je me demande si c'est pas parce que j'aurai raté celle d'avant. merci de votre aide d'avance.

Soit f la fonction définie sur R par f(x)=|-x²+2x+3|.

1. Dresser le tableau de variations de la fonction g : x --> -x²+2x+3.

j'ai trouvé 16 pour delta et -1 et 3 comme racine.

2.Résoudre dans R l'équation g(x)=0. En déduire le tableau de variations de f.

pour sa j'ai fait -x²+2x+3=-1(x+1)(x-3), j'ai obtenu -2x²+3x+10. Ensuite j'ai calculer delta (89) et j'ai trouver comme racine 3-√89/4 et 3+√89/4.

3. Dans un repère, tracer la représentation graphique de g. En déduire et tracer celle de f.

Pour ça j'ai utilisé ma calculatrice TI-82 et j'ai mis dans le repère -x²+2x+3 et -2x²+3x+10 et je l'ai refait sur ma feuille de brouillon.

4. Retrouver le tableau de variations par lecture graphique.

Sa je comprends pas car l'aide me dit d'utiliser la tangente cf mais quand je la calcule je trouve une droite mais qui n'est pas la tangente de cf et je comprends pas a quoi sert et qu'est-ce qu'une pente.

5. Étudier la dérivabilité de f en -1 par lecture graphique. justifier.

[mtschoon]

Bonsoir,

J'essaie de comprendre tes réponses...je pense qu'elles sont à revoir.

1. C'est le tableau de variation ( signe de g'(x) et sens de variation de g ) qui est demandé .
   Revois ce qu'il faut faire avec ton cours.

Tu dois trouver cela :

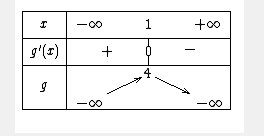
2. g(x)=0 <=> x=-1 ou x=3 (solutions de l'équation )

-1(x+1)(x-3) te donne -x²+2x+3.

Je ne vois vraiment pas ce qu'est ce -2x²+3x+10 ?

[mtschoon]

Pas de réponse au sujet de ce "-2x²+3x+10" ? ? ?

Comme je ne pourrai pas me connecter au forum pendant plusieurs jours, je te donnedes indications pour faire cet exercice.

La première chose est de revoir ton cours en général et la définition de "valeur absolue" en particulier.

Grâce à ma première réponse, tu peux trouver le signe de g(x) et le sens de variation de f

Pour x ≤ -1, g(x) ≤ 0 , donc f(x)=-g(x)
Vu que g est croissante, son opposée f est décroissante

Pour -1 ≤ x ≤ 1, g(x) ≥ 0, donc f(x)=g(x)
Vu que g est croissante, son égale f est croissante

Pour 1 ≤ x ≤ 3, g(x) ≥ 0, donc f(x)=g(x)
Vu que g est décroissante, son égale f est décroissante

Pour x ≥ 3, g(x) ≤ 0 , donc f(x)=-g(x)
Vu que g est décroissante, son opposée f est croissante

Tu résumes cela en faisant le tableau de variation de f

Pour les représentations graphiques, je te joins une image:

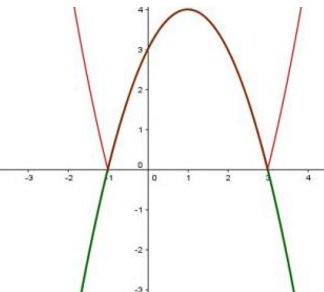
La représentation graphique de g (parabole) est en vert
La représentation graphique de f est en rouge

Bon travail.

[mtschoon]

J'ai oublié ladérivabilité à -1
Seulement unelecture graphique est demandée.

f serait dérivable en -1 si et seulement si la courbe (en rouge) admettrait une tangente (dont les coefficient directeur serait le nombre dérivé) au point (-1,0)
Ce n'est pas le cas, doncf n'est pas dérivable en -1.

Tu peux donner des précisions.
f n'est pas dérivable en -1, mais cependant elle est dérivable à gauche et à droite en -1 ( mais les nombres dérivés sont différents)

Par le point de coordonnées (-1,0), tu traces graphiquement les deux "demi-tangentes" à la courbe en rouge (représentation graphique de f).
Tu lis le mieux possible leurs coefficients directeurs.
Le nombre dérivé à gauche est -4
Le nombre dérivé à droite est 4

*Tout ceci nécessite que tu commences à approfondir ton cours...
*
Bon courage !