fonction - geogebra

Bonjour, pouvez vous m'expliquer comment on peut faire une figure dynamique de géogébra et m'expliquer ou me donner des exemples pour des questions que je n'ai pas compris pouvez vous regardez si j'ai fais des erreurs dans mon exercice merci d'avance

Pour cet exercice, une figure dynamique Geogeobra est demandée.

Dans un repère orthonormé, A est le point de coordonées (2;-1) et B le point de coordonées (2;0)

Le point K, distinct de B, est sur la demi-droite [BO]. La droite [AK] coupe l'axe des ordonnées en L et M est le milieux du segment [KL]. Dans cet exercice, on cherche à déterminer le lieu du point M quand le point K décrit la demi-droite [BO].

Faire une figure avec géogébra (à défaut construire 8 point M). Les points M semblent se déplacer sur une courbe C qui ressemble à celle d'une fonction de référence laquelle? (je n'ai pas réussi à faire le figure mais j'ai répondu au autre questions)

La courbe ressemble à une fonction inverse (une hypervole)

On appelle alpha l'abscisse du point K

Dans le cas où 0<alpha<2, exprimer la longueur OL en fonction d'alpha. En déduire l'ordonnée y du point M en fonction d' alpha.

Exprimer alpha en fonction de l'abscisse x du point M appartient à la courbe d'équation y=x/2-2x

J'utilise le théorème de Thales dans les triangles KOL et KBA

On sait que: Ko=alpha
KB=2-alpha
BA est parallèle OL
or: Ko/KB=LO/AB
alpha/(2-alpha)=LO/1

alpha=LO(2-alpha)
LO=alpha/(2-alpha)
Ordonnée du point L:alpha/(2-alpha)
Ordonnée du point K(alpha;0)
Donc l'ordonnée est la moitié du segment[KL]= YK + YL /2
L'ordonnée de M=alpha/2
M(alpha/2; alpha/2(2-alpha)
y=x/(2-2x)

On admet que l'ensemble des points M est la courbe C représentative de la fonction f définie sur]-∞; 1[ par f(x)= x/ 2-2x

a) Démontrer que, que tout x de l'intervalle]-∞;1[, on a -O,5+1/2-2x= f(x)
(je n'ai pas compris comment faire)

b)En déduire le sens de variation de la fonction f sur ]-∞; 1[
Le sens de variation ne change pas sauf si on multiplie par -2 sur x qui inverse le sens. On sait que la fonction y=1 est décroissante sur]-∞;0]. On déduit que la fonction est croissante sur]-∞;1[. Le sens de variation est inversé à cause de -2, on décale x de 1 à cause de x-1.

c) Expliquer géométriquement pourquoi pour tout x de]-∞;1[,on a f(x) >-0,5
(je n'ai pas réussi à faire cette question)

d) Tracer la courbe C

En vous remerciant d'avance cdt

Bonjour,

Ce que tu demandes est fort long !

Je pense qu'en cours, ton professeur t'a expliqué le maniement de Geogebra.

Je vais essayer de t'indiquer comment représenter le lieu

je te joins un schéma (c'est une impression d'écran ).
Il faudra que tu fasses la construction toi-même avec le logiciel.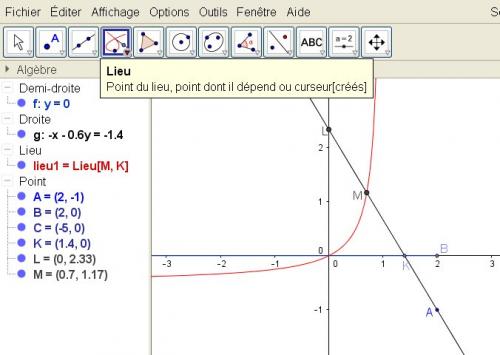

$fichier math$

Tu dois commencer à placer tous les éléments indiqués dans l'énoncé.
Ensuite, dans le menu horizontal, tu cliques sur la 4ème case (à partir de la gauche)
En bas de la colonne qui s'est ouverte, tu cliques surlieu
Tu cliques sur M (qui est le point du lieu)
Tu cliques sur K (qui est le point dont dépend le lieu)

Le lieu de M ce crée : courbe en rouge sur le schéma.
Il s'agit d'une branche d'hyperbole .

Pour "voir" ce qui se passe, tu fais glisser à la souris le point K sur la demi-droite [B0) et tu dois voir le point M se déplacer sur la courbe rouge.

Si j'ai un peu de temps, je vérifierai tes réponses (ultérieurement) ou peut-être que quelqu'un d'autre les vérifiera.

bonjour, merci de votre réponse et de votre aide j'ai du mal car je n'ai pas de professeur (je suis au CNED). cordialement

J'ai entendu dire que les cours du CNED étaient bons, mais les travailler seul(e) ne doit pas être facile !

Je regarde tes réponses.

C'est bon

2)a) le plus simple :

$−0,5+12−2x=−0.5(2−2x)+12−2x=...=f(x)-0,5+\frac{1}{2-2x}=\frac{-0.5(2-2x)+1}{2-2x}=...=f(x)$

2)b)

Tu as mal recopié.

Ce n'est pas la fonction y=1 qui est croissante mais la fonction définie par $y=1xy=\frac{1}{x}$

L'idée est juste mais il faudra clarifier un peu la rédaction.

2)c)

Tu peux utiliser la réponse à la 2)a) : elle a été faite pour cela

x < 1 donc 2-2x > 0 donc 1/(2-2x) >0

Vu que $f(x)=−0,5+12−2xf(x)=-0,5+\frac{1}{2-2x}$ , tu peux déduire que $\gt -0.5$

Graphiquement, la courbe sera au-dessus de la droite d'équation y=-0.5

Bon travail !

bonjour, grâce à votre aide j'ai compris mes erreurs et j'ai pu terminer l'exercice merci beaucoup cordialement

De rien !

A+

bonjour, excusez moi j'ai terminé l'exercice mais je pensais pouvoir faire la courbe. J'ai placer tout les éléments de l'énoncé mais la courbe c (le lieu) ne veut pas se tracer merci d'avance pour votre réponse. cordialement

Bonjour,

Désolée pour le retard relatif à ta dernière question (j'étais absente...)

Pour le lieu (la courbe) je te conseille de refaire exactement ce que je t'ai indiqué : c'est la manipulation normale.

Si tu n'y arrives pas, tu peux éventuellement faire construire la courbe avec son équation : $f(x)=x2−2xf(x)=\frac{x}{2-2x}$ pour x < 1

Pour cela, dans la case horizontale en dessous de la zone de graphique, tu tapes :

Fonction[x/(2-2x),-∞,1]

(Le symbole ∞ fait partie des caractères spéciaux que l'on obtient en cliquant sur α (à droite).

Evidemment, le mieux est de refaire la véritable manipulation pour obtenir le lieu.

Bonjour ,excusez moi je n'ai pas pu vous répondre avant merci j'ai réussi à faire la courbe cette fois, . merci de vos réponses et de vos explications .cordialement

C'est bien d'y être arrivé(e) !