complexes (interprétations géométriques)
-
AAnabelle2110 dernière édition par
Bonjour,
A tout point , on associe le nombre complexe :
z'= z−(1+2i)z−i\frac{z-(1+2i)}{z-i}z−iz−(1+2i)Pour le a) il s'agit de la médiatrice du segment AB. M ∈ à cette médiatrice privée du point A où A(i) et B(1+2i)
b) la partie imaginaire doit être égale à 0
z'= x+yi−1−2ix+yi−i\frac{x+yi-1-2i}{x+yi-i}x+yi−ix+yi−1−2i
= (x+yi−1−2i)(x−yi+i)(x+yi−i)(x−yi+i)\frac{(x+yi-1-2i)(x-yi+i)}{(x+yi-i)(x-yi+i)}(x+yi−i)(x−yi+i)(x+yi−1−2i)(x−yi+i)
= x2−xyi+xi+yix+y2+y−x+yi+i−2ix−2y+2(x+yi−i)(x−yi+i)\frac{x^{2}-xyi+xi+yix+y^{2}+y-x+yi+i-2ix-2y+2}{(x+yi-i)(x-yi+i)}(x+yi−i)(x−yi+i)x2−xyi+xi+yix+y2+y−x+yi+i−2ix−2y+2
= xi+yi−i−2xix2+(y−1)2\frac{xi+yi-i-2xi}{x^{2}+(y-1)^{2}}x2+(y−1)2xi+yi−i−2xi
= −x+y−1x2+(y−1)2\frac{-x+y-1}{x^{2}+(y-1)^{2}}x2+(y−1)2−x+y−1=0Mais franchement la je doute que ce soit ça...
-
mtschoon dernière édition par

Bonjour,
Oui pour le a)
Pour le b), ton calcul n'est pas bien rédigé car c'est z' que tu as mis sous forme algébrique et dans la même égalité tu n'as conservé que la partie imaginaire.
Tu aurais dû écrire
im(z′)=−x+y−1x2+(y−1)2im(z')=\frac{-x+y-1}{x^{2}+(y-1)^{2}}im(z′)=x2+(y−1)2−x+y−1
Je n'ai pas vérifié la partie réelle, mais cette partie imaginaire est bien exacte.
La condition−x+y−1x2+(y−1)2=0\frac{-x+y-1}{x^{2}+(y-1)^{2}}=0x2+(y−1)2−x+y−1=0 est exacte mais elle n'est pas suffisante.
C'est la condition pour que z' soit réel (positif ou négatif)
Tu pourrais dire que l'ensemble des points M pour que z' soit un réel est la droite d'équation**-x+y-1=0** ( privée des points A et B)
-
mtschoon dernière édition par

Piste pour le b)
Pour répondre au b), je te conseille d'utiliser l'interprétation géométrique de l'argument d'un quotient
z' réel strictement positif <=> arg(z')=0 (2∏)
arg(z′)=arg(z−(1+2i)z−i)=arg(zm−zbzm−za)arg(z')=arg(\frac{z-(1+2i)}{z-i})=arg(\frac{z_m-z_b}{z_m-z_a})arg(z′)=arg(z−iz−(1+2i))=arg(zm−zazm−zb)
La condition est donc :
arg(zm−zbzm−za)=0 (2π)arg(\frac{z_m-z_b}{z_m-z_a})=0\ (2\pi)arg(zm−zazm−zb)=0 (2π)
Tu traduis cette égalité en angle, tu places les points A et B dans le plan complexe et tu raisonnes (sans calculs).
Evidemment, tu obtiendras des portions de droite appartenant à la droite d'équation -x+y-1=0 qui passe par A et B
-
AAnabelle2110 dernière édition par
d'accord merci je vais essayer de comprendre
-
mtschoon dernière édition par

Bonne réflexion et tiens nous au courant si besoin.
-
AAnabelle2110 dernière édition par
j'ai déjà placé les points A et B dans un repère et j'obtiens un angle de 180° soit un angle de pi mais je n'arrive pas à voir comment je pourrais déterminer pour que z' soit un réel strictement positif à partir de cela ...
-
mtschoon dernière édition par

Je suppose que tu as traduit
arg(zm−zbzm−za)=0(2π)arg(\frac{z_m-z_b}{z_m-z_a})=0 (2\pi)arg(zm−zazm−zb)=0(2π)
par (ma⃗,mb⃗)=0 (2π)(\vec{ma},\vec{mb})=0\ (2\pi)(ma,mb)=0 (2π)
Réfléchis avec ça...(trace la droite (AB) pour t'aider)
-
AAnabelle2110 dernière édition par
Vu que (ma⃗\vec{ma}ma,mb⃗\vec{mb}mb) = pi (2pi)
Donc l'ensemble des points est le segment ouvert ]AB[ ?
-
mtschoon dernière édition par

Tu ne cherches pas M tel que (ma⃗,mb⃗)=π (2π)(\vec{ma},\vec{mb})=\pi\ (2\pi)(ma,mb)=π (2π)
Tu cherches M tel que (ma⃗,mb⃗)=0 (2π)(\vec{ma},\vec{mb})=0\ (2\pi)(ma,mb)=0 (2π)
Pour que(ma⃗,mb⃗)(\vec{ma},\vec{mb})(ma,mb) soit nul, les points A,B,M sont nécessairement alignés donc M est nécessairement sur la droite (AB)
Il faut savoiroù précisément.
Raisonne sur la droite (AB) pas seulement sur le segment [AB]
("Droite (AB)" veut dire "droite passant par A et B")
Pour être claire, la droite (AB) est composée de 3 parties (deux vertes et une rouge)
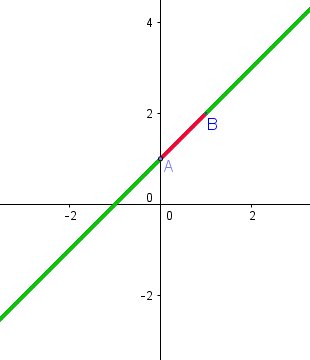
Place M dans différentes positions sur cette droite (AB) pour déduire ce qui convient et ce qui ne convient pas.
-
AAnabelle2110 dernière édition par
concernant la position de M il faut que son affixe soit un réel pur ? Je ne vois que M(-1) mais il s'agit d'un réel négatif
-
AAnabelle2110 dernière édition par
Soit M un point du plan d’affixe non nulle z
en fait M appartient à la droite (AB) mais privée du segment AB ?
-
mtschoon dernière édition par

Je te conseille de revoir le b) depuis le début, car tu t'égares.
Je crois que tu confonds z et z'
C'est z' qui doit réel ("pur" comme tu dis) strictement positif , et non z
z est un complexe que tu cherches pour que z' soit un réel strictement positif.
Si tu as compris l'interprétation graphique, l'image M de z est définie par :
(ma⃗,mb⃗)=0 (2π)(\vec{ma},\vec{mb})=0\ (2\pi)(ma,mb)=0 (2π)Lorsque M est choisi en dehors de la droite (AB), l'angle(ma⃗,mb⃗)(\vec{ma},\vec{mb})(ma,mb) n'est pas nul , donc l'extérieur de la droite (AB) ne convient pas.
Reste à étudier la droite (AB)
Lorsque M est entre A et B ( sur le segment
rouge), (ma⃗,mb⃗)=...(\vec{ma},\vec{mb})=...(ma,mb)=...
Lorsque M est sur une des demis droites en
vert, (ma⃗,mb⃗)=...(\vec{ma},\vec{mb})=...(ma,mb)=...Lorsque tu auras répondu à ces deux petites questions, tu pourras tirer la conclusion demandée au b) sur l'ensemble des points M cherché
-
mtschoon dernière édition par

Tu as répondu avant que je t'envoie ma réponse à ta proposition précédente !
L'ensemble des points M cherchés au b) est bienla droite (AB) privée du segment [AB] (c'est à dire la zone en vert sur le schéma)
-
AAnabelle2110 dernière édition par
Lorsque M est entre A et B ( sur le segment rouge) , (ma⃗\vec{ma}ma,mb⃗\vec{mb}mb)= pi/2 (2pi)
Lorsque M est sur une des demis droites en vert, (ma⃗\vec{ma}ma,mb⃗\vec{mb}mb)= pi (2pi)
Donc l'ensemble des points M cherché est la droite (AB) privée du segment AB
-
mtschoon dernière édition par

Tes deux dernières propositions sont inexactes...et elles contredisent la conclusion (exacte) indiquée...vu que tu cherches M pour que l'angle soit nul.
Ce n'est pas logique !Mets un point M sur le segment rouge et lis la mesure de l'angle qui va de ma⃗\vec{ma}ma à mb⃗\vec{mb}mb
Mets un point M sur une demi-droite verte et lis la mesure de l'angle qui va de ma⃗\vec{ma}ma à mb⃗\vec{mb}mb
Idem pour l'autre demi-droite verte.
Je ne comprends pas ce qui peux te gêner
-
AAnabelle2110 dernière édition par
quand M est sur le segment rouge l'angle vaut pi (2pi) et quand M est sur le'un des deux demi-droites vertes l'angle vaut 0 (2pi)
-
mtschoon dernière édition par

OUI ! ! !
Cette fois tout semble bon.
-
AAnabelle2110 dernière édition par
MERCI !!!

-
AAnabelle2110 dernière édition par
Encore une petite question la droite d'équation pour le a) est bien y = -x+2 ?
-
mtschoon dernière édition par

OUI.
-
AAnabelle2110 dernière édition par
ok
-
mtschoon dernière édition par

De rien !
