Equation - TVI

Bonjour , je suis en terminale sti2d et je faisait un marathon d'équation de toutes sortes (second troisième degré, réciproque, bicarré, ln et exp)
Et je me suis posé l'équation suivante :

$8/3)x-2^x$ =0

Par déduction une des solutions est 3 mais après avoir tourné en rond en utilisant les propriétés de calculs du logarithme népérien et exponentielle je commence à baisser les bras .

Pouvez vous m'aider à trouver une façon de résoudre cette équation ou bien n'y a t'il pas de réel méthode accessible à mon niveau
Merci

Bonsoir,

Par "calculs", tu ne pourras pas résoudre une telle équation.

La solution "évidente" est 3, l'autre solution est voisine de 0.55 (à la calculette)

Piste,

Tu peux poser $f(x)=83x−2xf(x)=\frac{8}{3}x-2^x$

Tu étudies les variations de f, puis tu utilises le théorème des valeurs intermédiaires .

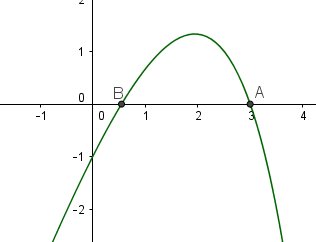
Je te joins la représentation graphique de f

Les solutions de l'équation sont les abscisses de A et B

$fichier math$

Excusez moi mais je ne connais pas ce théorème ou bien je le connaissais.
Pouvez vous m'éclairer ou bien de simple recherche internet me suffiront ?

Ps: J'ai fait mes recherches, j'ai donc trouvé que malgré le théorème TVI nous ne pourront pas obtenir une valeur exacte , est ce vrai ?

Ps2: Je dois donc étudier la fonction f sur l'intervalle [0;1] où je verrais qu'elle est strictement croissante et continu pour ensuite appliqué le TVI et trouver une valeur approcher . Je ne connais pas la dérivé de $k^x$ , j'ai essayé de la trouver par le calcul est ce bien $k^x$ lnk ?

Je te mets un lien pour le TVI
(regarde le cas d'une fonction strictement monotone sur un intervalle)

http://www.parfenoff.org/pdf/Term_S/analyse/Term_S_Continuite_theor_val_interm.pdf

Sur un intervalle où la fonction est continue et strictement monotone, le TVI permet de prouver l'existence et l'unicité de la solution de l'équation mais non la valeur exacte de cette solution.
(On utilise le TVI lorsque qu'il n'est pas possible de déterminer la valeur exacte par calcul )

Un conseil : cherche le sens de variation de la fonction sur R et sur chacun des deux intervalles où elle est strictement monotone, utilise le TVI.
Ensuite, travaille à la calculette.

La dérivée que tu proposes est bonne.

Bien sûr, ton professeur t'expliquera tout cela en détail et plus clairement.

Je trouve donc : ln(8/3ln2)/ln2) environ = 1,94
f'(x)= 8/3 $2^x$ ln(2)
f' est strictement positive sur ]-∞;(ln(8/3ln2)/ln2)] et strictement négative sur [(ln(8/3ln2)/ln2);+∞[ j'en déduis alors que
f est strictement croissante sur ]-∞;(ln(8/3ln2)/ln2)] et strictement décroissante sur [(ln(8/3ln2)/ln2);+∞[ or f est une fonction polynôme donc continue et lim f =-∞ pour x qui tend vers -∞ et f(1,94) >0 donc on en déduis que :
Sur ]-∞;(ln(8/3ln2)/ln2)] il existe un unique réel c tel que f(c)=0
Avec c environ égale à 0,5485

Merci pour votre aide , j'en parlerais a mon professeur pour plus de détails car le TVI n'est pas dans mon programme , c'est bien dommage.

Ce que tu as fait est bon sur ]-∞, ln(8/3ln2)/ln2) ] mais il faut aussi le faire sur [ln(8/3ln2)/ln2) , +∞[ pour prouver l'existence et l'unicité de la solution.
Ainsi, comme 3 est solution, tu peux assurer que sur cet intervalle, c'est la seule.

Tu auras prouvé que l'ensemble S des solutions de l'équation est :

$S=α,3S={\alpha,3}$ avec α ≈ 0.5485

Très bien!
Merci pour tout

De rien et bon marathon d'équations !