démontrer que des droites sont parallèles
-
Ssarouille33 dernière édition par
Bonjour,
je suis en première S et j'aurai besoin d'aide svpABCD est un carré. On place les points E et F à l'extérieur du carré de sorte que les triangles CDE et DAF soient équilatérales.
Démontrer que les droites (AC) et (EF) sont parallèles
je pense utiliser les vecteurs ...merci d'avance
-
mtschoon dernière édition par

Bonjour,
La première chose à faire, c'est un bon schéma.
Au besoin, je t'en joins un.
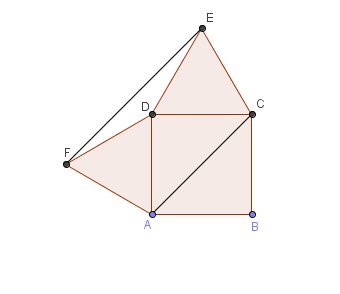
J'ignore le cours que tu es en train de traîner en ce moment...
Une méthode possible : faire des calculs d'angles.
En degrés, tu peux trouver (après calculs) que :
ace^\widehat{ace}ace vaut 105°
cef^\widehat{cef}cef vaut 75°Ces angles sont "internes" d'un même côté de la sécante (EC)
Comme ils sont supplémentaires (leur somme vaut 180°), les droites (AC) et (EF) sont parallèles.Bons calculs.
-
Ssarouille33 dernière édition par
Pour l'angle CEF on justifie sa valeur en disant que ces angles sont internes ?
-
mtschoon dernière édition par

Ce que tu dis n'est pas clair...
As-tu calculé les valeurs des deux angles que je t'ai indiqués ?
Si tu les as calculés, tu n'as plus qu'à conclure.
Si tu ne les as pas calculés, il faut le faire.
-
Ssarouille33 dernière édition par
pour ACE: ABCD est un carré donc ses angles valent 90°
DEC est un triangle équilatéral donc ses angles valent 60°
90°+60° =150°Pour CEF: les triangles CDE et DAf sont équilatéraux et ont donc leurs segments de même longueurs soient FD=DE donc FDE est isocèle en D.
L'angle FDE =60°+60°+90°=210 360-210=150
Or la somme des angles d'un triangle est égale à 180 donc 180-150=30
30/2=15 donc les angles DFE et DEF =15°15°+60°=75° pour CEF
voila mon raisonnement sans toutes les justifications
-
mtschoon dernière édition par

cef^\widehat{cef}cef est bon (75°)
ace^\widehat{ace}ace n'est pas bon ; ce n'est pas 90°+60°
-
Ssarouille33 dernière édition par
oui c'est 45+60=105 pardon
mais ensuite je ne sais pas comment montrer qu'elles sont parallèles enfin pas avec des angles supplémentaires
-
mtschoon dernière édition par

Si l'on sait que les angles" internes d'un même côté" sont supplémentaires (somme = 180°), alors on peut affirmer que les droites concernées sont parallèles.
Cela fait partie des propriétés vues, en principe, en Collège.
-
Ssarouille33 dernière édition par
je ne vois vraiment pas ...
-
mtschoon dernière édition par

Les angles calculés sont à l'intérieur de la bande limitée par les droites (AC) et (FE) : on dit qu'ils sont internes
Ils sont du même côté de la sécante (EC) ; on peut dire qu'ils sont co-internes.
Comme deux angles co-internes sont supplémentaires, tu peux déduire que : (AC)//(FE)
Si tu ne connais pas cette propriété, tu peux aussi utiliser des angles alterne-internes (égaux) ou des angles correspondants (égaux) en construisant des demi-droites en plus et tirer la même conclusion.