Difficulté de lecture / Livre de géométrie (grand public)
-
KKubdekubor dernière édition par
Bonjour à tous.
J'ouvre ce sujet pour vous demander un peu d'aide quant à un problème que je rencontre dans la lecture d'un livre de géométrie grand public (que j'ai emprunté dans une médiathèque).
Pour ceux que ça intéresse, il s'intitule :
La Géométrie classique : objets et transformations, et son auteur est Benoît Rittaud (agrégé de mathématiques).Donc, je vous présente problème, cela parle de comparaison de secteurs angulaires.
A un moment dans le livre, plusieurs définitions sont posées :
-
Un angle est la donnée de deux demi-droites (les côtés de l'angle) de même origine (le sommet de l'angle).
-
Un angle détermine deux secteurs angulaires, chacune des deux régions du plan dont l'angle en constitue la frontière est un secteur angulaire.
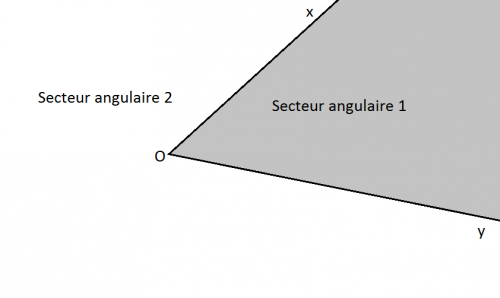
Cette image réalisée avec paint a été faite par moi.
On voit bien la différence entre un angle qui est formé par deux lignes et un secteur angulaire qui est une partie du plan.- Deux secteurs angulaires sont adjacents revient à dire qu'ils ont le même sommet et qu'ils ont pour seule partie commune un de leur côté.
Et puis ils parlent d'une propriété
- On peut comparer deux secteurs angulaires adjacents, l'un étant dit plus petit que l'autre lorsqu'il lui est inclus.
Maintenant la question à 10 000 francs
 ...
...Comment parmi deux secteurs angulaires adjacents (= dont l'intersection correspond seulement à leur côté commun, leur demi-droite commune) il peut y en avoir un qui soit inclus dans l'autre ?
Est-ce qu'il y a une erreur dans le livre ?Merci d'avoir lu !
-
-
Ssophie90 dernière édition par
Bonsoir,
je ne veux pas trop m'avancer les professeurs te répondrons certainement de façon plus précise.
-une petite piste a explorer .
en faites tes deux secteurs sont eux même inclus dans un autre secteur( cercle 360° en exemple)
nécessairement le plus petit est inclus ds le plus grands etc ,d'ailleurs c 'est comme les ensembles mathématique N⊂Z.....⊂R on peut dire N⊂R-On peut même dire que chaque secteur est inclus dans lui même ce qui est logique..
bon courage
-
mtschoon dernière édition par

Bonjour,
J'invente...donc aucune certitude...
Il semble que Benoît Rittaud ait voulu définir de façon **"matérielle"**une relation d'ordre dans l'ensemble des secteurs angulaires.
En bref, dans ce sujet, les secteurs angulaires n'ont pas un place fixée dans le plan ; on peut imaginer qu'ils sont découpés dans un morceau de carton, seulement posés sur un plan, déplaçables et "retournables" .
Soit S1 un secteur angulaire délimité par [Ox) et[ Oy)
Soit S2 un secteur angulaire adjacent délimité par [Oy) et [Oz)On ne bouge pas S1
On fait un "retournement" de S2 autour de [Oy)Après ce "déplacement", si [Oz) se retrouve ainsi à l'intérieur du secteur angulaire S1, S2 est alors inclus dans S1 et on dit que S2 est plus petit que S1.
Voilà l'idée que j'ai pour étayer l'explication car je ne crois pas que Benoît Rittaud puisse se tromper . Comme le manuel est pour "grand public", l'explication qu'il a donnée est très "concrète"...
-
jb2017 dernière édition par
Je ferai deux remarques.
Il faut se poser où est l'intérêt d'une telle définition pour un livre grand public
mais je n'irai pas plus loin car je ne connais pas ce livre.
D'autre part, mathématiquement parlant, je ne vois pas de problème
à ce que l'on introduise une relation d'ordre qui n'est pas totale .
-
mtschoon dernière édition par

Moi non plus je n'ai pas lu le livre...
J'ai seulement vu la couverture à Amazone !Si l'idée proposée est bonne (???) , je suppose qu'il n'y a pas de problème pour prendre deux secteurs angulaires (où qu'ils soient posés), les positionner pour les rendre adjacents, en retourner un pour le comparer à l'autre comme indiqué, et obtenir un ordre total.
Kubdekubor, qui a dû lire, le livre nous expliquera peut-être l'intérêt...
-
KKubdekubor dernière édition par
Merci pour vos réponses.
D'après ce que j'ai compris, vous dites (sophie90 et mtschoon) que pour comparer les deux secteurs angulaires adjacents, il faut utiliser une isométrie (déplacement ou retournement) pour inclure l'un des deux secteurs dans l'autre, je suis d'accord sur ce point, mais je ne suis pas d'accord avec la propriété de Benoît Rittaud.
Grosso modo, l'axiome que vous aviez utilisez pour comparer les deux secteurs angulaires adjacents (sophie90 et mtschoon), c'est :
A et B sont deux secteurs angulaires, (A ⊂ B) ⇔ (A < B) .
Et ensuite vous avez déplacez les deux secteurs comme l'a décrit mtschoon.
Je reprend la propriété de Mr. Rittaud :
- On peut comparer deux secteurs angulaires
adjacents, l'un étant dit plus petit que l'autre lorsqu'il lui est inclus.
"adjacents" est un mot inutile.
On aurait très bien pu marquer :
- On peut comparer deux secteurs angulaires, l'un étant dit plus petit que l'autre lorsqu'il lui est inclus.
Le but de la propriété est d'indiquer dans quel cas on peut comparer deux secteurs.
La vraie question, c'est de savoir : Pourquoi l'auteur a rajouté cette précision ?Pour répondre à votre question sur l'intérêt d'écrire une telle définition dans un livre grand public, c'est d'expliquer comment comparer des angles, c'est tout.
Vous aviez parlez de "relation d'ordre " et de "relation d'ordre totale", également.
Malheureusement mon niveau (= 2e générale) ne me permet pas de vous parler de ça, je suis navré, je ne connais pas ces concepts.A la limite, vous pouvez tenter de m'expliquer cela...
- On peut comparer deux secteurs angulaires
-
mtschoon dernière édition par

Citation
Je reprend la propriété de Mr. Rittaud :- On peut comparer deux secteurs angulaires adjacents, l'un étant dit plus petit que l'autre lorsqu'il lui est inclus.
"adjacents" est un mot inutile.
On aurait très bien pu marquer :
- On peut comparer deux secteurs angulaires, l'un étant dit plus petit que l'autre lorsqu'il lui est inclus.
Je ne veux pas être l'avocat de Mr. Rittaud, mais je crois comprendre pourquoi il parle "d'adjacents"
Effectivement Kubdekubor, si S2 est inclus dans S1 , pas besoin que ces secteurs soient "adjacents" pour conclure que S2 < S1
Mais, ce n'est pas le seul cas.
Imagine qu'après retournement, on mette [Oy) à l'intérieur de S1 et que [Oz) soit à l'extérieur de S1 : dans ce cas, on ne peut pas tirer de conclusion (pour savoir si S2 < S1 ou non)Avec S1 et S2 adjacents, on peut parfaitement faire la comparaison.
En bref, il faut bien que les secteurs soient mis en position "d'adjacents" pour que le principe de Mr Rittaud fonctionne dans tous les cas.
-
mtschoon dernière édition par

Je mets deux schémas comme exemples avec des secteurs non adjacents.
Le secteur S1 est teinté en rouge
Le secteur S2 est hachuré en bleuDans ces cas, sans outil ( tel qu'un compas ou un rapporteur) et sansvision parfaite (du genre "avoir un compas dans l'oeil"), on ne peut comparerrigoureusement (et mathématiquement) S1 et S2.
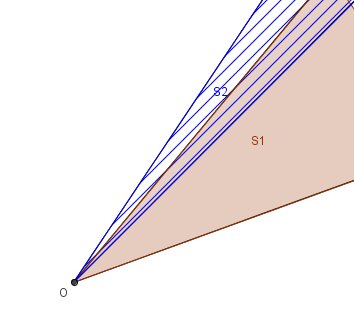
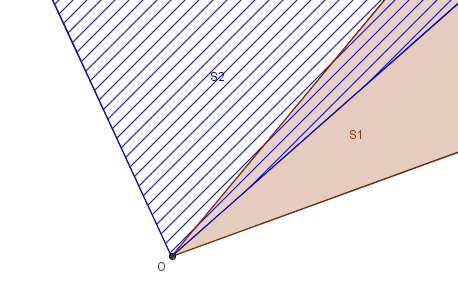
Le but de mettre ces secteurs en position adjacente permet de faire la comparaison de façon rigoureuse sans outil de mesure et sans approximation visuelle : c'est le principe qu'à utilisé Mr Rittaud.
-
KKubdekubor dernière édition par
Je vous remercie beaucoup mais je n'y comprends rien, je suis navré.
-
mtschoon dernière édition par

Désolée, mais peut-être qu'après réflexion ça ira mieux.
De toute façon, tu peux poursuivre la lecture du livre (même si tu ne vois toujours pas l'intérêt de la méthode de l'auteur...)
Bonne journée !