Je vous remercie beaucoup mais je n'y comprends rien, je suis navré.

Merci pour vos réponses.

D'après ce que j'ai compris, vous dites (sophie90 et mtschoon) que pour comparer les deux secteurs angulaires adjacents, il faut utiliser une isométrie (déplacement ou retournement) pour inclure l'un des deux secteurs dans l'autre, je suis d'accord sur ce point, mais je ne suis pas d'accord avec la propriété de Benoît Rittaud.

Grosso modo, l'axiome que vous aviez utilisez pour comparer les deux secteurs angulaires adjacents (sophie90 et mtschoon), c'est :

A et B sont deux secteurs angulaires, (A ⊂ B) ⇔ (A < B) .

Et ensuite vous avez déplacez les deux secteurs comme l'a décrit mtschoon.

Je reprend la propriété de Mr. Rittaud :

• On peut comparer deux secteurs angulaires
  adjacents, l'un étant dit plus petit que l'autre lorsqu'il lui est inclus.

"adjacents" est un mot inutile.

On aurait très bien pu marquer :

• On peut comparer deux secteurs angulaires, l'un étant dit plus petit que l'autre lorsqu'il lui est inclus.

Le but de la propriété est d'indiquer dans quel cas on peut comparer deux secteurs.
La vraie question, c'est de savoir : Pourquoi l'auteur a rajouté cette précision ?

Pour répondre à votre question sur l'intérêt d'écrire une telle définition dans un livre grand public, c'est d'expliquer comment comparer des angles, c'est tout.

Vous aviez parlez de "relation d'ordre " et de "relation d'ordre totale", également.
Malheureusement mon niveau (= 2e générale) ne me permet pas de vous parler de ça, je suis navré, je ne connais pas ces concepts.

A la limite, vous pouvez tenter de m'expliquer cela...

Bonjour à tous.

J'ouvre ce sujet pour vous demander un peu d'aide quant à un problème que je rencontre dans la lecture d'un livre de géométrie grand public (que j'ai emprunté dans une médiathèque).
Pour ceux que ça intéresse, il s'intitule :
La Géométrie classique : objets et transformations, et son auteur est Benoît Rittaud (agrégé de mathématiques).

Donc, je vous présente problème, cela parle de comparaison de secteurs angulaires.

A un moment dans le livre, plusieurs définitions sont posées :

• Un angle est la donnée de deux demi-droites (les côtés de l'angle) de même origine (le sommet de l'angle).

• Un angle détermine deux secteurs angulaires, chacune des deux régions du plan dont l'angle en constitue la frontière est un secteur angulaire.

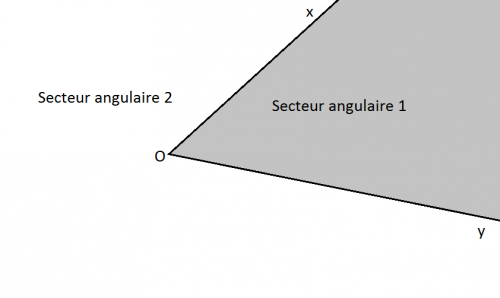
Cette image réalisée avec paint a été faite par moi.
On voit bien la différence entre un angle qui est formé par deux lignes et un secteur angulaire qui est une partie du plan.

• Deux secteurs angulaires sont adjacents revient à dire qu'ils ont le même sommet et qu'ils ont pour seule partie commune un de leur côté.

Et puis ils parlent d'une propriété

• On peut comparer deux secteurs angulaires adjacents, l'un étant dit plus petit que l'autre lorsqu'il lui est inclus.

Maintenant la question à 10 000 francs ...

Comment parmi deux secteurs angulaires adjacents (= dont l'intersection correspond seulement à leur côté commun, leur demi-droite commune) il peut y en avoir un qui soit inclus dans l'autre ?
Est-ce qu'il y a une erreur dans le livre ?

Merci d'avoir lu !