Fonctions Etude avec paramètre

Bonjour à tous

j 'ai besoin de votre aide
j'ai commencé cet exo mais je bloque :

b est un nombre réel et f fonction définie par :
f(x)= 2x+b/3x+5

on nous demande en fonction du paramètre b de déterminer le tableau de variation

donc j'ai commencé ainsi

f'(x)=2(3x+5)-(2x+b)3/(3x+5)^2
=6x+10-6x-3b/(3x+5)^2
=10-3b/(3x+5)^2

3x+5=0
3x=-5
x=-5/3

10-3b=0
10=3b
b=10/3

merci à vous pour votre aide

Bonjour,

Si tu n'utilises pas le Latex, mets suffisamment de parenthèses

Je suppose qu'il s'agit de $f(x)=2x+b3x+5f(x)=\frac{2x+b}{3x+5}$

f définie (et dérivable) sur Df = R / {-5/3}

La dérivée est exacte .

Vu que le dénominateur est strictement positif sur Df (car c'est un carré), f'(x) sera du signe du numérateur

Tu dois voir les cas 10-3b=0 , 10-3b > 0 , 10-3b < 0

Bonjour

je ne comprends pas

Je détaille

1er cas 10-3b = 0 <=> 3b = 10 <=> b = 10/3

f'(x) = 0 doncf constante sur ]-∞, -5/3[ et sur ]-5/3,+∞[

2ème cas 10-3b > 0 <=> 3b < 10 <=> b < 10/3

f'(x )> 0 donc f croissantesur ]-∞, -5/3[ et sur ]-5/3,+∞[

3ème cas 10-3b < 0 Tu continues.

donc 3ème cas b infé 3/10
donc f est décroissant sur ]-inf,-3/5[et sur ]-3/5,+inf[

je suis perdue
comment dois je ensuite faire le tableau des valeurs

Pour le 3éme cas, tu as fait une erreur sur b

Je détaille

10-3b < 0 <=> -3b < -10 <=> 3b > 10 <=>b > 10/3

f est décroissante sur ]-∞,-5/3[et sur ]-5/3,+∞[

Ah oui

et comment dois je présenter le tableau

Regarde peut-être ton cours pour voir comment se fait un tableau de variation.

Tu dois ici , faire 3 tableaux : un tableau par cas.

Pour chaque tableau :

Une ligne pour x avec -∞....-5/3.....+∞
Tu fais une double barre verticale en dessous de -3/5, vu que cette valeur est "interdite"

Une ligne pour f'(x) (suivant les cas, dans les deux cases vides , ce sera 0 OU + OU -)

Une ligne pour f (suivant les cas, dans les deux cases vides , ce sera flèche horizontale, OU flèche montante OU flèche descendante.)

je sais comment faire un tableau mais là dans ce cas je ne vois pas et en plus faire 3 tableaux?

Pour la 1ère ligne je suis ok pour - inf -5/3 et + inf
ensuite je ne vois pas du tout comment présenter

Relis les explications données ci-dessus et réfléchis.

Il y a 3 cas suivant b, donc 3 tableaux de variations suivant b

cas b = 10/3 : f constante sur les 2 intervalles séparés par -5/3
cas b < 10/3 : f croissante sur les 2 intervalles séparés par -5/3
cas b > 10/3 : f décroissante sur les 2 intervalles séparés par -5/3

désolé ca je comprends mais je ne vois pas comment faire le tableau

si je prends le 1er cas

1ère ligne
x - inf -5/3 + inf
b=10/3 + +
f(x) → →

Tu ne dois pas mettre b=10/3 au beau milieu du tableau !
(c'est f'(x) qui devrait être écrit)

Je te joins le sas b < 10/3 (fait au brouillon)

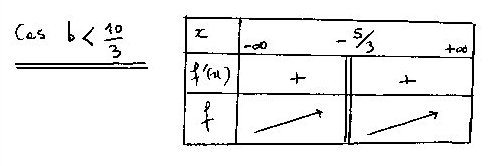
$fichier math$

pour cas b=10/3

c'est le même tableau

pour le cas b sup 10/3
donc f'(x) - (double barre) et -
f 2 fleches vers le bas

Pour b=10/3 , il faut que tu revois.

Dans ce cas, comme déjà dit, f'(x) vaut constamment 0( et c'est pour cela que f est constante) ( si tu remplaces b par 10/3 dans l'expression de f(x), tu trouves que f(x) vaut constamment 2/3, pour x≠-5/3)

Dans les deux cases relatives à f'(x), tu dois mettre 0 , et des flèches horizontales dans les 2 cases relatives à f

Pour le cas b > 10/3, ce que tu indiques est bon

merci à vous pour toutes ces explications
bonne soirée

De rien et revois tranquillement cet exercice car ce paramètre b semble te poser des problèmes.

Bonne soirée à toi.