équations (et inéquation) trigonométriques
-
CChucky6220 dernière édition par
Bonjour ,
j'ai un problème pour résoudre des équations trigonométriques . Le voici :
- cos(3x+π/6) = cos(x-π/3) dans R.
- cos(x+π/3) = sin(2x) dans [0;2π]
3)-√3/2 ≤ sin(2x) ≤ -1/2 dans [0;2π]
4)4cos(x)²-2(√3+1)cos(x)+√3=0 dans R
Pour la 1) , j'ai trouvé -π/4 et pour les autres , je suis bloquer et je ne sais pas quel méthode utiliser , merci pour votre aide

-
mtschoon dernière édition par

Bonjour,
J'ai l'impression que tu as QUATRE problèmes ( pas UN) !
Piste pour la 1)
La valeur -∏/4 est exacte mais on te demande toutes les solutions sur R , par une seule.
Principe (regarde ton cours) :
cosa=cosb <=> a=b+2k∏ ou a=-b+2k∏ (k entier)
Tu as donc deux équations à résoudre , en remplaçant a par 3x+∏/6 et b par x-∏/3
Tiens nous au courant si besoin.
-
CChucky6220 dernière édition par
Pour la 1)
cos(a) = cos(b) si et seulement si il existe k ∈ Z tel que b = a + 2kπ ou il existe k ∈ Z tel que b = −a + 2kπ
• sin(a) = sin(b) si et seulement si il existe k ∈ Z tel que b = a + 2kπ ou il existe k ∈ Z tel que b = π − a + 2kπ3x+π/6=x-π/3 + 2kπ ou 3x+π/6= -(x-π/3) + 2kπ
pour la première solution j'ai bien trouvé -π/4 , et la deuxième π/24
Est ce correct ?
-
CChucky6220 dernière édition par
Pour la réponse 2)
j'ai utilisé l'identité : cos (x) = sin(∏/2+x)
J'ai trouver les solutions ci ,$\textit\frac{x=12n\pi +\pi}{6} ; \frac{x=12n\pi+\pi}{18}$
Est ce que cela est correct ?
-
mtschoon dernière édition par

Je regarde ta 1) que tu as modifiée
Ce n'est pas "il existe k" c'est "pour tout k , k appartenant à Z
Après calculs et simplifications, je t'indique les réponsesde la 1)
x=−π4+kπx=-\frac{\pi}{4}+k\pix=−4π+kπ
x=π24+2kπ4=π24+kπ2x=\frac{\pi}{24}+\frac{2k\pi}{4}=\frac{\pi}{24}+\frac{k\pi}{2}x=24π+42kπ=24π+2kπ
-
CChucky6220 dernière édition par
Pour la question 3) , je ne sais pas du tout comment procéder , comment faire ?
-
mtschoon dernière édition par

Ne brule pas les étapes !
Je regarde tes réponses à la 2)
Tu peux utiliser la formule proposée.
Cela te donne pour équation à résoudre :
sin(π2+x+π3)=sin2x\sin(\frac{\pi}{2}+x+\frac{\pi}{3})=\sin 2xsin(2π+x+3π)=sin2x
c'est à dire
sin(x+5π6)=sin2x\sin(x+\frac{5\pi}{6})=sin2xsin(x+65π)=sin2x
Vérifie ta première réponse écrite
Sauf erreur, pour tout k de Z
x=5π6−2kπx=\frac{5\pi}{6}-2k\pix=65π−2kπ
x=π18+2kπ3x=\frac{\pi}{18}+\frac{2k\pi}{3}x=18π+32kπ
Ce n'est pas fini !
L'énoncé te demande les solutions sur [0,2∏]
Il faut donc que tu trouves les solutions sur cet intervalle (cherche les valeurs de k qui conviennent)
-
mtschoon dernière édition par

Piste pour la 3)
Travaille par lecture graphique avec le cercle trigonométrique et les angles remarquables ayant pour sinus -1/2 et -√3/2
Place les points M et M' du cercle trigonométrique d'ordonnées -1/2
Place les points N et N' du cercle trigonométrique d'ordonnées -√3/2Les solutions cherchées , pour 2x, sont représentées par les secteurs colorés du schéma joint.
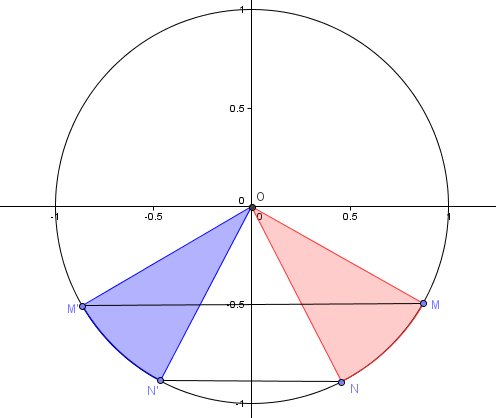
Lorsque tu auras les réponses pour 2x ( sur [0,4∏], tu en déduiras les solutions pour x sur [0,2∏]
-
CChucky6220 dernière édition par
Donc j'ai fais mes reccherche pour la 3) , j'ai trouvé ∏/12 +k∏ et 3∏/4+k∏
Est ce bon ?
Pour la 4) , j'ai trouvé cos(x) = √3/2 ou cos(x) = 1/2
Est ce bon ?
-
mtschoon dernière édition par

Pour la 3), j'ignore ta démarche, mais ce que tu donnes ne peut pas être l'ensemble des solutions d'une double inéquation sur [0,2∏].
Pour la 4), je suppose que tu as fait un changement d'inconnue pour résoudre une équation du second degré.
Tes réponses pour cosx sont bonnes, mais ce n'est pas terminé.
Il te reste à déduire les valeurs de x solutions sur R