3. Suites numériques 2

Suites numériques 2

  • J

    Jai un énorme problème avec mon exo de math:

    On considère (Un) définie par U0= 0 et Un+1 = 3un+2/Un+4

    1. la suite un est elle bien définie ?
    2. que peut on conjecturer pour la suite Un ?
    3. on admet que 0 <Un < 1 , en déduire les variations de la suite
    4. on considère la suite Vn= Un-1/Un+2
      A) prouver que V (n) est une suite géométrique de raison 2/5
      B) calculer V0 et Vn puis en fonction de n
      C) exprimer Un en fonction de Vn, puis en fonction de n
      D) en déduire la limite de suite Un

    Alors 1) oui la suite est bien défini car on a la première terme et la raison pour passer au terme suivant
    2) je n'est pas du tout trouve
    3) la suite est croissante ?
    4) a) j'ai réussi cette question
    B) v0 = -1/2 , Vn = vo × 1/5n ?
    La c) et d) Je ne sais pas du tout

    mtschoon 1 réponse
  • mtschoon

    BONJOUR !

    Tu as des indications ici que tu peux exploiter.

    http://www2.ac-lyon.fr/lyc01/cotiere/IMG/pdf/Corrige_DS3_TS6.pdf

    J 1 réponse
  • J

    Pouvez vous m'aider pour la 4c et 4d svp..

    Je n'y arrive pas

    mtschoon 1 réponse
  • mtschoon

    Les 4)c) et 4d) sont traitées à l'Exercice 1 questions 2)a) et 2)b) du lien que je t'ai proposé.

    Va consulter et reposte si besoin.

    S 1 réponse
  • S

    Bonsoir ,juliiien

    Je vous propose un raisonnement légérement différent , en complément de ce fichier.Peut être que vous pourrez y voir plus clair.

    Dèja pour la 3)

    u<em>n+1−u</em>n=3u<em>n+2u</em>n+4−u<em>n=−u2</em>n−u<em>n+2u</em>n+4=−(u2<em>n+u</em>n−2)un+4{ u }<em>{ n+1 }-{ u }</em>{ n }=\frac { { 3u }<em>{ n }+2 }{ { u }</em>{ n }+4 } -{ u }<em>{ n }=\frac { { -u^{ 2 } }</em>{ n }-{ u }<em>{ n }+2 }{ { u }</em>{ n }+4 } =\frac { -\left( { u^{ 2 } }<em>{ n }+{ u }</em>{ n }-2 \right) }{ { u }_{ n }+4 }u<em>n+1−u</em>n=u</em>n+43u<em>n+2​−u<em>n=u</em>n+4−u2</em>n−u<em>n+2​=un​+4−(u2<em>n+u</em>n−2)​

    $\leftrightarrow \frac { -\left( { u }{ n }-1 \right) \left( { u }{ n }+2 \right) }{ { u }_{ n }+4 } \$ (1)(1)(1)

    En partant de l'indication donnée dans l'énoncé vs prouvez assez facilement que cette quantité (1)(1)(1)est positive .. donc la suiteun{ u }_{ n }un​ est croissante.

    4A
    v<em>n+1=1−3u</em>n+1+2=1−35u<em>n+10u</em>n+4=5u<em>n−3u</em>n+10−125u<em>n+10=2(u</em>n−1)5(un+2){ v }<em>{ n+1 }=1-\frac { { 3 } }{ { u }</em>{ n+1 }+2 } =1-\frac { 3 }{ \frac { { 5u }<em>{ n }+10 }{ { u }</em>{ n }+4 } } =\frac { { { 5u }<em>{ n }-3u }</em>{ n }+10-12 }{ { 5u }<em>{ n }+10 } =\frac { { 2\left( { u }</em>{ n }-1 \right) } }{ 5\left( { u }_{ n }+2 \right) }v<em>n+1=1−u</em>n+1+23​=1−u</em>n+45u<em>n+10​3​=5u<em>n+105u<em>n−3u</em>n+10−12​=5(un​+2)2(u</em>n−1)​

    $\leftrightarrow { v }{ n+1 }=\frac { 2 }{ 5 } .{ v }{ n },\quad \quad \$donc${ v }_{ n }={ \left( \frac { 2 }{ 5 } \right) }^{ n }.\left( -\frac { 1 }{ 2 } \right) \$

    4C

    c 'est juste un travail de transformation en partant devnv_nvn​,jusqu' àunu_nun​

    ${ v }{ n }=1-\frac { 3 }{ { u }{ n }+2 } \quad \quad \rightarrow \quad 1-{ v }{ n }=\frac { 3 }{ { u }{ n }+2 } \quad \rightarrow { u }{ n }=\frac { 3 }{ 1-{ v }{ n } } -2\quad \$

    ↔u<em>n=1+2v</em>n1−vn\leftrightarrow { u }<em>{ n }=\frac { 1+2{ v }</em>{ n } }{ 1-{ v }_{ n } }↔u<em>n=1−vn​1+2v</em>n​

    4D

    C'est assez immédiat puisque v<em>n{ v }<em>{ n }v<em>n est une suite géométrique de raison ∣q∣≺1\left| q \right| \prec 1∣q∣≺1, ainsi v</em>n⟶ 0{ v }</em>{ n }\longrightarrow\ 0v</em>n⟶ 0

    donc,lim⁡<em>n→∞u</em>n=1\lim <em>{ n\rightarrow \infty } u</em>{ n }=1lim<em>n→∞u</em>n=1

    bonne continuation

    J 1 réponse
  • J

    Mais pour la 2) , je ne vois pas qu'est ce que je peux conjecturer pour cette suite...

    mtschoon 1 réponse
  • mtschoon

    Pour la 2), pour pouvoir conjecturer, il faut que tu calcules (à la calculette ou autre ) U1U_1U1​, U2U_2U2​, U3U_3U3​, U4U_4U4​, U5U_5U5​,...et que tu observes les valeurs trouvées.
    Tu pourras ainsi conjecturer sur quel intervalle semble appartenir les termes, le sens de variation de la suite, sa limite.

    Evidemment, ce ne seront que des observations et les questions suivantes sont là pour les démontrer.

    J 1 réponse
  • J

    Pour U1 je trouve 2 , U2 = 0.77 , U3 = 0.907
    Je ne trouve pas de lien entre cela..

    mtschoon 1 réponse
  • mtschoon

    Revois U1U_1U1​
    Avec seulement 3 valeurs, tu ne peux pas conjecturer grand' chose...

    Pour vérifier tes valeurs, je te joins les valeurs approchées de U1U_1U1​ à U16U_{16}U16​ et à partir de U17U_{17}U17​, le programme arrondi à 1

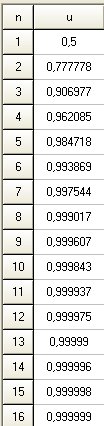
    fichier math

    Evidemment, c'est à toi de faire avec l'outil que tu as à ta disposition.

    J 1 réponse
  • J

    Donc qu'est ce que je peux conjecturer a partir de de cela ?

    mtschoon 1 réponse
  • mtschoon

    Observe les valeurs trouvées et tire toi-même des conclusions.

    J 1 réponse
  • J

    Mais est ce que les miennes sont bonne ?

    mtschoon 1 réponse
  • mtschoon

    Tu parles des valeurs ou des conclusions ?

    Pour les valeurs : compare tes valeurs avec celles que je t'ai données

    U1U_1U1​ est faux (c'est 0.5 et non 2), U2U_2U2​ et U3U_3U3​ sont bons
    (ce sont des valeurs approchées bien sûr)

    Pour les conclusions :

    Observe sur quel intervalle sont les valeurs de la suite (n'oublie pas que U0U_0U0​=0)
    Observe si, lorsque n augmente, les valeurs de la suite augmentent ou diminuent (d'où le sens de variation conjecturé)
    Observe vers quel nombre les valeurs de la suite s'approchent , lorsque n augmente (d'où la limite conjecturée)

Se connecter pour répondre