Compléter l'arbre et calculer les probabilités d'événements
-
Jjen78 dernière édition par Hind
Bonjour, j'aurais besoin de savoir si mon exercice est correct et avoir une explication si possible pour une question, voici mon exercice:
Une boîte contient 6 boules rouges et n boules blanches. Les boules sont indiscernables au toucher. Un jeu consiste à tirer successivement, sans remise, 2 boules de la boîte. Si les 2 boules ont la même couleur, je joueur gagne 1 euro, si elles sont de couleurs différentes, le joueur perd 1 euro.- Dans cette question on prend n=3
a. Compléter l'arbre suivant:
première ligne: 2/3 R→5/8 R
→ 2/8 B
deuxième ligne: 3/9 B → 5/8 R
→ 2/8 B
b. Calculer les probabilités d'obtenir
-2 boules de même couleur
-2 boules de couleurs différentes
pour le premier je trouve 1/2
pour le deuxième j'ai fais 1- P("2boules de même couleurs") qui me fait également 1/2
c. On note X la variable aléatoire qui à chaque tirage de 2 boules, associe le gain algébrique du joueur. Déterminer la loi de probabilité de X et calculer son espérance mathématique E(X). Que remarque-t-on ? Que peut-on dire du jeu ?
J'ai fais 1*1/2+(-1)*1/2 ce qui me fait 0 mais je ne suis pas sur de moi
2. Dans cette question, l'entier n est quelconque supérieur ou égal à 2
a. Exprimer en fonction de n, les probabilités des événements X=1 et X=-1
Pour X=1 je trouve 30+n(n-1)/(6+n)(5+n)
Pour X=-1 je trouve 1- 30+n(n-1)/(6+n)(5+n)
b. Déterminer la loi de probabilité de X et montrer que E(X)= (n²-13n+30)/(n+6)(n+5)
Je trouve le bon résultat
c.Pour quelles valeurs de n, le jeu est-il équitable ?
Je trouve pour n=3 et n=10
d.Pour quelles valeurs de n, le jeu est-il défavorable au joueur ?
Je trouve que c'est défavorable pour n appartenant à {4;5;6;7;8;9}
Je voudrais juste savoir si c'est correct et si ce n'est pas le cas avoir des explications pour comprendre mes erreurs, merci d'avance !
- Dans cette question on prend n=3
-
mtschoon dernière édition par

Bonjour,
Je viens de regarder le début de tes réponses.
A la question 1), je crois voir des erreurs relatives aux valeurs sur l'arbre.Pour plus de clarté, je te joins l'arbre.
Merci de dire si tu comprends (ou pas) les valeurs écrites.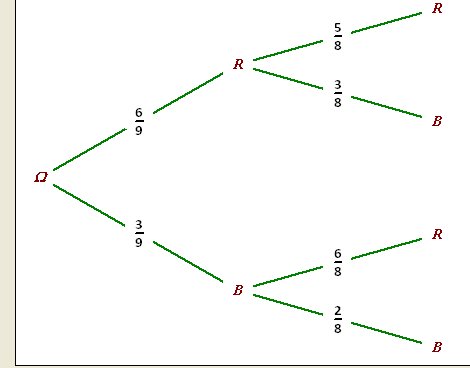
-
Jjen78 dernière édition par
Bonjour, je comprend l'arbre or il y a deux valeurs que justement non, le 3/8 et le 6/8, pourquoi c'est cela et pas 2/8 et 5/8 ?
-
mtschoon dernière édition par

Explication pour le 3/8
Sachant qu'une boule a été prise, il reste à choisir une boule parmi 8
Cette boule blanche est à choisir parmi 3 vu qu'il y a toujours 3 boules Blanches (la boule déjà prise étant Rouge)
D'où la probabilité 3/8
Explication pour le 6/8
Sachant qu'une boule a été prise, il reste à choisir une boule parmi 8
Cette boule Rouge est à choisir parmi 6 vu qu'il y a toujours 6 boules Rouges (la boule déjà prise étant Blanche)
D'où la probabilité 6/8
REMARQUE :
Tes erreurs n'ont pas eu d'influence sur la probabilité d'obtenir deux boules de couleurs différentes car tu ne t'en es pas servi. Tu es passé par l'évènement contraire.Si tu avais calculé cette probabilité avec p(R,B)+p(B,R), tu aurais obtenu un résultat inexact et tu t'en serais aperçu car la somme des probabilités n'aurait pas valu 1.
-
Jjen78 dernière édition par
Bonjour, d'accord je comprend ton raisonnement. En effet vers la fin je me suis rendue compte pour la 1c. Je ne trouvais pas 1
Pour celle ci vu que c'est la dernière où je bloque, pour l'espérance je trouve 0
Que remarque t-on ? Que peut-on dire du jeu ? Cela veut dire qu'en moyenne les personnes gagnent 0€ ?
-
mtschoon dernière édition par

Pour la 1)c), ta réponse est bonne
E(X)=0
Cela prouve que le jeu est équitable
Tes réponses pour la 2) sont exactes.