Suites et algorithme

Bonsoir

J'ai besoin de votre aide
Je suis bloqué sur cet exo

On note Vn l'effectif de vautours pour l'année 2016+1 avec n nombre entier naturel. Il ne restait environ 1000 vautours en 2016 soit V0=1000
Hypôthèse que 2% des vautours meurent chaque année

V0=1000
V1=1080
V2=1158
V3=1235

1- Exprimer Vn en fonction de n - etablir que pour tout entier naturel n,Vn+1=098Vn+100
J'ai fait
Vn+1=Vn-2/100Vn+100
= 0.98Vn+100

2- Démontrer que la suite Un définie pour tout entier naturel n par Un=Vn-5000 est une suite géométrique dont on précisera la raison et le premier terme
J'ai commencé ainsi
Un=Vn-5000
Un+1=Vn+1-5000
=0.98Vn+100-5000
=0.98Vn-4900

et la je bloque

3- Exprimer Un puis Vn en fonction de n

Merci à vous pour votre aide car j'ai encore d'autres questions à traiter à la suite de celles-ci

Bonjour,

Je suppose que tu n'as pas écrit toutes les données car il n'y a pas d'explication sur ce "+100" ...

J'admets donc (sans preuve) que $v_{n+1}=0.98v_n+100$

Piste pour la 2)

Tes calculs sont justes mais il faut continuer en exprimant $V_n$ en fonction de $U_n$

$u_n=v_n-5000$ donc $v_n=u_n+5000$

d'où

$u_{n+1}=0.98v_n-4900=0.98(u_n+5000)-4900$

Tu développes, tu simplifies et tu dois trouver

$u_{n+1}=0.98u_n$

(Un) est la suite géométrique de premier terme U0 (que tu calcules) et de raison 0.98

Tu pourras écrire que $u_n=u_0(0.98)^n$ puis en déduire l'expression de $V_n$ en fonction de n

Essaie de poursuivre.

Bonsoir

Donc pour Vn je trouve
= -3920*0.98n+5000

Ensuite j'ai 2 dernières questions et là je ne sais pas du tout comment les traiter

Expliquer pourquoi l'intervalle ]4500:5500[ contient tous les termes Vn à partir d'un certain rang à préciser
Pour info dans une de mes premières questions, j'ai du calculer les valeurs jusque N=200
Rédiger un algo donnant le rang à partir duquel les termes Vn appartiennent à un intervalle du type ]5000-a;5000+a[ où a est un réel positif

Encore merci à vous

Je ne comprends pas la valeur -3920 que tu donnes .

D'après ton énoncé, $v_0=1000$ et $u_n=v_n-5000$ d'où $u_0=v_0-5000$

Au final, $u_0=1000-5000=-4000$

Cela change l'expression de $V_n$

Vérifie cela avant de poursuivre les questions.

bonsoir

oui je me suis trompée

Vn=-4000+5000=1000

pouvez vous m 'aider pour les suivantes

Idée pour l'intervalle I=]4500,5500[

$v_n=-4000(0.98)^n+5000$

Cette suite est à termes positifs, croissante;
Lorsque n tend vers +∞, 0. $98^n$ tend vers 0 donc $V_n$ tend vers 5000.
Pour des grandes valeurs de n, $V_{n }$ appartient donc à un intervalle centré sur 5000.
A vrai dire, $V_n$ appartient à la partie gauche de cet intervalle I.

Ma calculette me donne
V102≈4490,5
V103≈4500,7

Donc $V_{n }$ appartient à I pour n ≥ 103

Vérifie avec ta calculette.

Idée pour l'algorithme avec I=]5000-a,5000+a[

$V_n$ sera dans la partie gauche de l'intervalle (raison indiquée précédemment)

Pour faire simple, la condition $V_n$ > 5000-a sera suffisante.

Inspire toi de l'algorithme donné dans l'énoncé de ton précédent exercice.

Je te joins un algorithme possible fait avec Algobox ( gratuit et que tu peux télécharger). Il est commode car on peut tester l'algorithme et voir ainsi les erreurs éventuelles.
Evidemment, écris l'algorithme avec les habitudes de ton professeur.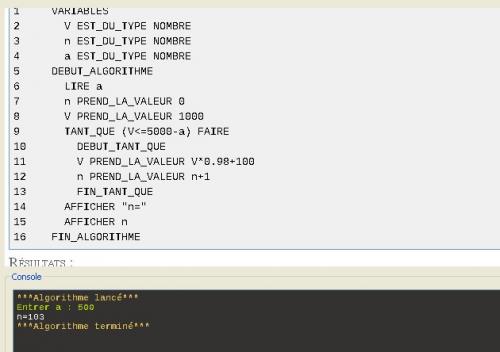

$fichier math$

Bon travail !

Ok merci pour votre aide

je vais essayer de refaire un algo

De rien !

A+