Fonction carré

Bonjour,
je dois faire un exercice mais je ne comprends rien du tout
Voici l'énoncé

Merci d'avance

Bonjour Chrosmiq75,

Indique tes éléments de réponse et la question qui te pose problème.
a) Ecris h(x) - k(x) et factorise.

x- $x\sqrt{x}$
Facteur = $x\sqrt{x}$
Donc $x\sqrt{x}$ x - ( $x\sqrt{x}$ -1) ?

Pourquoi x - ?
Le - est en trop.

Salut,

Il y a une erreur dans l'énoncé.

Il faut remplacer le $h : x$ --> $V x$ par $k : x$ --> $V x$ (avec $V$ pour le signe radical (racine carrée))

Et donc : $h (x) - k (x) = x - V x$

Continue ...

Bonjour,

J'espère Chrosmiq75 que tu as tenu compte des informations qui t'ont été données.

Je vois que tu as scanné l'énoncé. J'ignore si cela est autorisé sur le "nouveau" forum. Je m'informerai.
Cet énoncé est d'ailleurs très mal écrit.
En plus de la confusion entre h et k à la question 1)a) , la question 1)c) n'a pas de sens .Il faut supprimer le "que"

Vu ta réponse pour la 1)a) je doute que tu aies vraiment compris...
J'explicite un peu
Pour $\ge 0\ \ x=\sqrt x \times \sqrt x$
$h(x)−k(x)=(x×x)−xh(x)-k(x)=(\sqrt x \times \sqrt x)-\sqrt x$
Pour t'aider à la factorisation, tu peux écrire
$h(x)−k(x)=(x×x)−(x×1)h(x)-k(x)=(\sqrt x \times \sqrt x)-(\sqrt x\times 1)$
En mettant $x\sqrt x$ en facteur, tu obtiens
$h(x)−k(x)=x(x−1)h(x)-k(x)=\sqrt x (\sqrt x -1)$

Piste pour la 1)b)
Tu dois résoudre $x−1≥0\sqrt x -1 \ge 0$
Nécessairement $\ge 0$ pour que $x\sqrt x$ soit calculable (dans l'ensemble des nombres réels)

En transposant : $x≥1\sqrt x \ge 1$

Vu qu'il s'agit d'une inégalité entre nombres positifs, tu peux élever chaque membre au carré sans changer le sens de l'inégalité.
Tu trouves ainsi $\ge ...$
Je te laisse poursuivre.

Reposte si besoin.

Voici l'illustration graphique, pour t'éclairer.

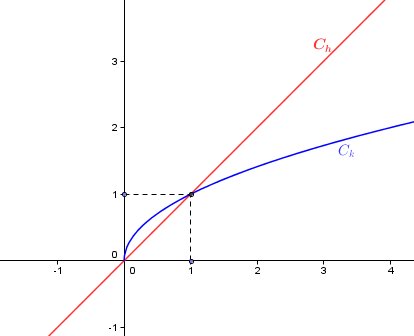
Bon travail.

Bonsoir,
Merci à tout le monde pour votre aide, mais du coup je suis perdu, l'énonce que j'ai est faux?
Du coup la 1) a) C'est
$x\sqrt{x}$ ( $x\sqrt{x}$ -1) ?

Donc pour 1) b)
On doit comme vous l'avez dit resoudre $x\sqrt{x}$ -1 ≥ 0
Donc, je deplace -1 a droite c'est à dire $x\sqrt{x}$ ≥ 1
Apres je mets au ², donc $(x)2(\sqrt x) ^2$ ≥ 1²
Alors, x ≥ 1
Je pense que c'est ça mais j'ai du mal à rédiger...

Ah oui d'accord j'ai vu l'erreur dans l'énoncé

Bonsoir chrosmiq75

Ecris l'énoncé de la question ou se trouve l'erreur.

@noemi a dit dans Fonction carré :

Ecris l'énoncé de la question ou se tr

Je ne sais pas si j'ai le droit de mettre un énoncé scanné ?

Non pas de scan, écris l'énoncé.

Exercice1 : Soit les fonctions h : x→x et h: x→√x .
On note Ch et Ck leurs courbes représentatives dans un même repère.

a. Montrer que, pour x≥0 , h(x )−k (x )=√ x(√x−1) .
b. Résoudre l’inéquation √x−1≥0 .
c. En déduire que, pour x≥0 , le signe de h(x) – k(x) et la position relative des courbes
Ch et Ck .
A l’aide des résultats de la question 1), comparer, pour x≥0 , √x et x .

Cet énoncé comprend toujours les erreurs indiquées précédemment.

Bonsoir,
Chrosmiq75, je confirme : après avoir demandé l'information auprès de l'Administrateur de ce nouveau forum, comme dans l'ancien, les scans d'énoncés ne sont pas autorisés.

Ta réponse à la 1)b) est bonne .

Evidement, Noemi voulait que tu rectifies les fautes de cet énoncé.!

Bon travail.

@mtschoon La façon dont j'ai répondu est bonne aussi?
Pouvez vous me guider pour la c svp?

Je te l'ai déjà dit : Ta réponse à la 1)b) est bonne .

Commence par corriger les deux fautes de l'énoncé comme te le demande Noemi.
Ensuite, nous t'aiderons pour la 1)c)

Bonne nuit!

Pour l'étude du signe de h(x) - k(x) étudie le signe du produit.

Énoncé corrigé ?
Exercice1 : Soit les fonctions h : x et k: x→√x .
On note Ch et Ck leurs courbes représentatives dans un même repère.

a. Montrer que, pour x≥0 , h(x )−k (x )=√ x(√x−1) .
b. Résoudre l’inéquation √x−1≥0 .
c. En déduire pour x≥0 , le signe de h(x) – k(x) et la position relative des courbes
Ch et Ck .
A l’aide des résultats de la question 1), comparer, pour x≥0 , √x et x .

Bonjour chrosmiq75

L'énoncé est bien corrigé.

Bonjour,

Oui, ça fait vraiment plaisir de lire un énoncé bien écrit !

Pour la 1)c), Noemi t'a déjà donné la piste.

Grâce au résultat de la question 1)a) , tu étudies le signe du produit $x(x−1)\sqrt x(\sqrt x -1)$ pour $\ge 0$

Plusieurs cas sont à prévoir.
$x\sqrt x$ est toujours positif pour x positif (tu peux séparer le cas x > 0 du cas x=0)
Grâce au résultat de la question 1)b) , tu sais que $x−1\sqrt x -1$ est positif si et seulement si x est supérieur à 1 (tu peux séparer le cas x > 1 du cas x=1)

En bref, pour faire un travail soigné, tu peux distinguer 4 cas :
1er cas : x = 0
2ème cas : 0 < x < 1
3ème cas : x =1
4ème cas: x > 1

Je te détaille un peu le 4ème cas :
x > 1 donc $x−1\sqrt x-1$ > 0
Vu que $x\sqrt x$ > 0, on multiplie deux expressions strictement positives donc $x(−1)\sqrt x(\sqrt -1)$ > 0 donc h(x)-k(x) > 0

A toi de faire les 3 autres cas.

Bonjour,

Pour la question 1 c, tu peux présenter les résultats dans un tableau.

Je suis complètement perdu la...

Chrosmiq75 précise ce que tu ne comprends pas .
Pour étudier le signe du produit, tu peux faire un tableau de signes.

Je ne sais pas comment faire pour trouver le signe ainsi que la position

Chrosmiq75, as-tu compris la résolution de la question 1 b) ?
Si tu construis un tableau de signes :
première ligne : x 0 1 + $∞\infty$
deuxième ligne : $x\sqrt{x}$ avec la valeur qui annule et le signe dans chaque intervalle
troisième ligne : $x−1\sqrt{x}-1$ avec la valeur qui annule l'expression et le signe dans chaque intervalle
Je te laisse réaliser le tableau.

Comme ça le tableau ?

Chrosmiq75 c'est un bon début.
Il manque + $∞\infty$ dans la première ligne, et
la quatrième ligne qui est le produit.
Tu complètes par le signe - ou + pour chaque intervalles

Je rajoute +∞ apres le 1?
C'est quoi le produit ?
D'accord et je mets des 0 aussi ?

Oui, après le 1.
Le produit : $x\sqrt{x}$ ( $x−1\sqrt{x}-1$ )
Oui tu mets 0 quand l'expression s'annule.

@noemi a dit dans Fonction carré :

x\sqrt{x}x
(x−1\sqrt{x}-1x
−1 )

D'accord merci je vais essayer de le faire je vous redis

L'énoncé indique x ≥ 0 donc la partie à gauche de 0 est inutile. De plus elle est en partie fausse pour x < 0, $x\sqrt{x}$ n'existe pas.

La dernière ligne est fausse : + x + donne + !

J'enleve donc √x et les signes sous 0 ?

Tu supprimes la deuxième colonne, celle ou tu as mis que des -.
Puis tu modifies les signes de la dernière ligne. Le signe se calcule par le produit des signes des deux lignes précédentes

par - donne ...... et
par + donne .......

Complète et rectifie.

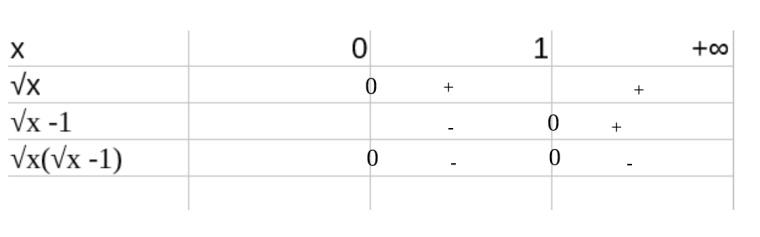
Comme ça ?

Juste une erreur la dernière colonne

fois + donne +

Du signe de h(x) - k(x), tu déduis si la courbe Ch est au dessus ou en dessous de la courbe Ck.

@noemi a dit dans Fonction carré :

Juste une erreur la dernière colonne

fois + donne +

Du signe de h(x) - k(x), tu déduis si la courbe Ch est au dessus ou en dessous de la courbe Ck.

C'est vrai je le sais en plus erreur inattention

pour tout x ∈ R, Ch est strictement au dessous de Ck ?

Non chrosmiq75,
Ch est au dessus de Ck pour x appartenant à l'intervalle ou le signe de h(x)-k(x) est strictement positif.

à l'intervalle ]1;+∞[ ?

Oui c'est cet intervalle.
Sur l'autre intervalle Ch est .......

au dessous de Ck pour xE]0;1[ ?

Oui, c'est juste.

D'accord merci,
Pour la 2) je dois dire quoi?

Pour la question 2), Comparer $x\sqrt{x}$ et x revient à comparer k(x) et h(x).
Sur quel intervalle k(x) > h(x) ?
Sur quel intervalle k(x) < h(x) ?
pour quelles valeurs de x k(x) = h(x) ?

k(x) > h(x) sur xE]0;1[
k(x) < h(x) sur ]1;+∞[
k(x) = h(x) pour x = 1 ?

k(x) = h(x) pour x = 0 et x = 1,
tu remplaces k(x) par $x\sqrt{x}$ et h(x) par x

Quand je remplace les résultats que j'ai dit ne changent pas ?

Chrosmiq75 ,
Ce que tu as écrit est juste.
Comme k(x) = $x\sqrt{x}$ et h(x) = x
pour $x$ $∈\in$ ]0;1[ k(x) > h(x), alors $x\sqrt{x}$ > $x$
pour ....

Ahh d'accord !
pour xE]1;+∞[, k(x) < h(x) alors $x\sqrt{x}$ < ${x}$
pour x=0 et x=1, k(x) = h(x) alors $x\sqrt{x}$ = ${x}$

C'est correct.

Merci pour votre aide !