Primitive

[nirmalaa]

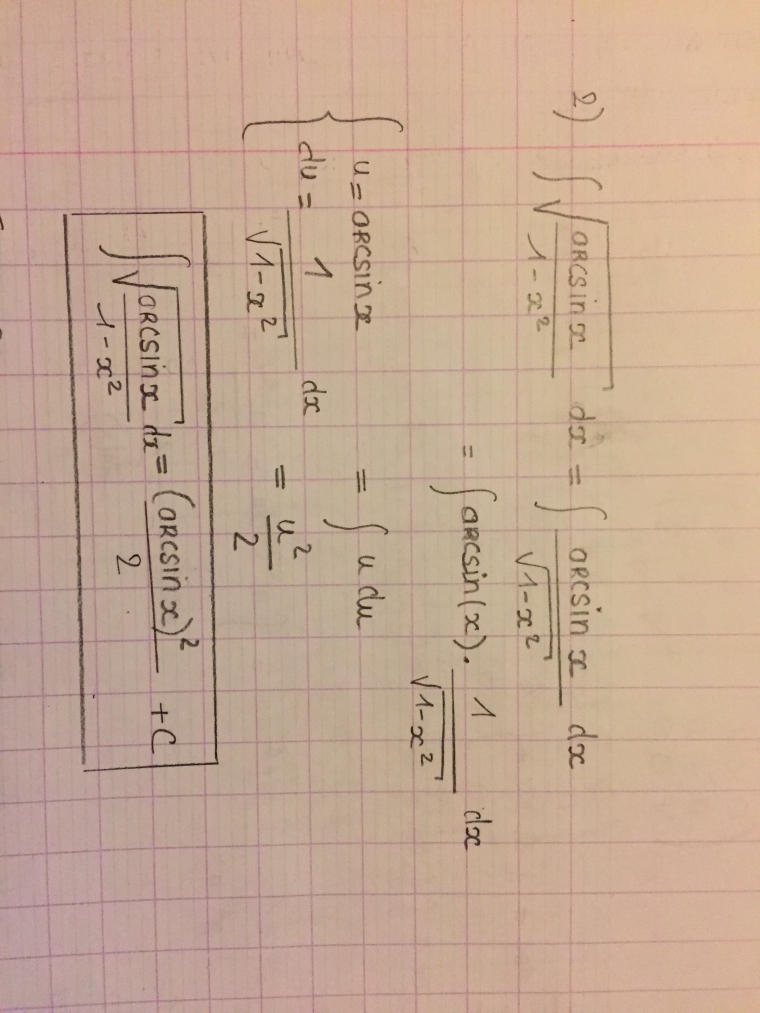
Bonjour, j’ai une primitive à calculer, je vous les joint. Je voudrai savoir si c’est bon. Merci de votre aide

[mtschoon]

Bonjour,

Si la fonction est $\frac{arcsinx}{\sqrt{1-x^2}}$, ton calcul est bon mais $\sqrt{\frac{arcsinx}{1-x^2}}$ n'est pas égal à $\frac{arcsinx}{\sqrt{1-x^2}}$.
Alors, on ne sait pas vraiment quelle est la fonction à intégrer...
(arcsinx fait-il partie du radicande ou non ? )

S'il s'agit d'intégrer $\frac{arcsinx}{\sqrt{1-x^2}}$, c'est bon
S'il s'agit d'intégrer $\sqrt{\frac{arcsinx}{1-x^2}}$, ce n'est pas bon

Vérifie ton énoncé et tiens nous au courant.

[nirmalaa]

J’ai bien la deuxième intégrale sur mon énoncé !

[Casebas]

Bonjour @nirmalaa ,

Le scan d'énoncé n'est pas autorisé sur le forum
Tu as toutes les explications sur ce topic pour écrire l'énoncé joliment avec de belles expressions mathématiques afin que l'on puisse te répondre comme il faut !
Bonne journée et bonne année !

[mtschoon]

Merci Casebas pour ce rappel !
J'espère que nirmalaa en tiendra compte.

nirmalaa , il s'agit donc de $\sqrt{\frac{arcsinx}{1-x^2}}$

Si ce n'est pas indiqué dans la question, tu dois préciser l'ensemble sur lequel tu travailles (ici [0,1[)

En posant u=arcsinx, $u^{\prime }=\frac{1}{\sqrt{1-x^2}}$
$du=\frac{1}{\sqrt{1-x^2}}dx$
Tu as donc à chercher les primitives de $\sqrt{u}du$, c'est à dire de $u^{\frac{1}{2}}du$

Pour cela, utilise la formule usuelle:
une primitive de $u^{n}du$ est $\frac{u^{n+1}}{n+1}$ (pour n différent de -1)