PROBLÈME DE COÛT
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
Bonjour, j'ai un problème à résoudre mais je bloque.
Dans une entreprise fabriquant des objets en bois, le coût de fabrication, en milliers
d’euros, de x milliers d’objets est donné par : C(x )=x3x^3x3−6x26x^26x2+13x• Le coût moyen de production est le quotient du coût total C(x) par la quantité x :
CM(x)=C(x)/x
.
• Les quantités qui permettent d’égaliser les coûts avec les recettes sont appelées points morts
de la production : le bénéfice est nul.
• La plage de bénéfice est l’intervalle dans lequel le bénéfice algébrique est positif ou nul, ou
lorsque le coût moyen est inférieur ou égal à la recette unitaire.a. Calculer le coût de fabrication de 2 000 objets, c’est-à-dire C(2).
b. Vérifier que, pour tout réel x : C(x )=(x−2)²+x+8 .
c. En utilisant la somme de deux fonctions, démontrer que la fonction C est strictement
croissante sur [0;+∞[.a. Calculer le coût moyen de production quand l’entreprise fabrique 1 000 objets, 2 000
objets, 4 000 objets.
b. Exprimer le coût moyen CM(x) en fonction de x.
c. Déterminer le minimum de CM et la valeur en laquelle il est atteint.- Chaque objet est vendu 5€.
a. Résoudre l’équation CM(x) = 5 .
En déduire les points morts de la production.
b. Résoudre l’inéquation C M≤5 .
En déduire la plage de bénéfice de l’entreprise.
Ce que j'ai fait :
1)
a) C(2) : 232^323-6x222^222+13*2
C(2) : 10
Donc le coût de fabrication pour 2000 objets et de 10 000 €.b) C(x)=(x3x^3x3-3x²(-2)+3x(-2²)-232^323) +x+8
=x3x^3x3+6x²+12x-8+x+8
=x3x^3x3+6x²+13xc) je ne comprends pas.
a)
1000 objets : CM(1) = C(1)/1 = 8/1 = 8
2000 objets : CM(2) = C(2)/2 = 10/2 = 5
4000 objets : CM(4) = C(4)/4 = 20/4 = 5b) ?
c) ?- ?
- Chaque objet est vendu 5€.
-
Bonjour Chrosmiq75,
Vérifie l'énoncé de la question 1 c.
-
Pour la question 2 b), Ecris en fonction de x l'expression C(x) / x puis tu la simplifies.
Pour la question 2 c) Etudie la fonction trouvée à la question 2 b), allure de la courbe, fonction de référence, ....
-
?Un Ancien Utilisateur dernière édition par
Oui j'ai vérifié le c) c'est bien ça.
J'ai bon pour ce que j'ai fait?2b)
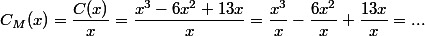 x²-6x+13 ?
x²-6x+13 ?
-
L'expression de Cm(x) est juste.
Etudie cette fonction, type de fonction, sens de variation, ...Pour la question 1 c) quelles sont les variations de la fonction g(x) = (x−2)2(x-2)^2(x−2)2
-
?Un Ancien Utilisateur dernière édition par
Décroissante puis croissante ?
-
Oui, mais précise le domaine de croissance et de décroissance.
-
?Un Ancien Utilisateur dernière édition par
Je ne comprends pas ?
-
?Un Ancien Utilisateur dernière édition par
x3x^3x3−6x26x^26x2+13x est croissante sur IR
et (x−2)3(x-2)^3(x−2)3+x+8 est egalement croissante car le coefficient directeur est supérieur a 0?
-
Bonjour Chrosmiq75,
Rectifie l'erreur dans l'énoncé question 1 c. pour C(x) c'est exposant 3 !
Tu décomposes ensuite en deux fonctions strictement croissantes pour démontrer que la fonction C est strictement croissante.