3. limite de la fonction gamma en 0

limite de la fonction gamma en 0

  • C

    Bonjour,
    je dois trouver la limite de la fonction gamma en 0. Je ne dois pas utiliser la relation entre gamma de x et gamma de x+1x+1x+1 car la démo est demandée dans les questions d'après.
    Je pense qu'il faut minorer gamma de xxx par l'intégrale entre 0 et 1 et ensuite minorer exp(−t)exp(-t)exp(−t).
    Cependant je ne sais pas par quoi minorer et je n'arrive pas au résultat ( je trouve comme limite 0 et j'ai lu que c'était + l'infini).
    Merci
    Celine

  • N
    Modérateurs

    Bonjour celine,

    Ton raisonnement est correct. Indique tes calculs.

  • mtschoon

    Bonjour,

    Je vois Céline que tu t'es adressé précédemment à plusieurs forums pour tenter d'avoir de l'aide.
    Ce que tu as écrit, ce n'est pas ce que tu as fait mais ce qu'on t'a dit....et tu ne sais pas quoi faire...d'où ton absence de réponse ici...

  • mtschoon

    Pour conjecturer la limite de de la fonction Gamma en 0 (par valeurs positives), tu peux commencer par consulter la représentation graphique de cette fonction "spéciale". Elle est peut-être dans ton cours.
    Je te joins son allure (c'est seulement son allure...faite avec quelques points)
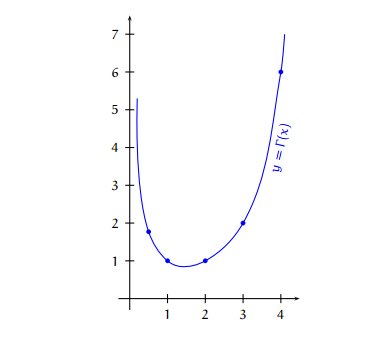
    0_1515056607993_gamma.jpg
    Tu peux constater que la limite est bien +∞\infty∞

    Maintenant, il faut le prouver.

  • mtschoon

    Essaie de minorer comme "on t'a dit" .

    ∫0+∞tx−1e−tdt>∫01tx−1e−tdt\displaystyle\int_0^{+\infty}t^{x-1}e^{-t}dt \gt \displaystyle \int _0^1 t^{x-1}e^{-t}dt∫0+∞​tx−1e−tdt>∫01​tx−1e−tdt

    Sur [0,1], tu peut minorer e−te^{-t}e−t par une constante positive

    t∈[0,1]t\in[0,1]t∈[0,1] donc et∈[1,e]e^ t \in [1,e]et∈[1,e] donc e−t∈[e−1,1]e^{-t} \in [e^{-1},1]e−t∈[e−1,1]

    D'où

    ∫01tx−1e−tdt>e−1∫01tx−1dt\displaystyle\int _0^1 t^{x-1}e^{-t}dt \gt e^{-1}\displaystyle\int _0^1t^{x-1}dt∫01​tx−1e−tdt>e−1∫01​tx−1dt

    Une primitive de tx−1t^{x-1}tx−1 est txx\frac{t^x}{x}xtx​ (pour x non nul)

    Tu dois pouvoir justifier que la dernière intégrale écrite a pour limite +∞+\infty+∞ lorsque x tend vers 0 (par valeurs positives) et tirer la conclusion souhaitée.

    Remarque : je n'aime guère manipuler ces intégrales "convergentes" pour lesquelles les justifications ne sont pas toujours à la hauteur...
    J'aurais préféré, par une IPP, utiliser la méthode qui n'est pas autorisée par ton énoncé...

    Bon courage.

Se connecter pour répondre