Série de Fourier - graphe
-
Rraphael3 dernière édition par
Bonjour nous venons d'attaquer les series de Fourier après les matrices.
Vous m'aviez été d'une grande aide pour les matrices donc je me permets de revenir vers vous.Je n'ai quasiment rien compris à ce chapitre mais en cherchant un peu, je suis arrivé à noter 2/3 éléments.
Par exemple) Déterminer, sans aucun calcul, le spectre de la fonction périodique de période 1
f: t-> 2sin(10 pi t)+ cos(20 pi t)
En utilisant Euler je trouve |C5|=1comment faut-il tracer le graphe par la suite?
Merci
-
Bonsoir raphael3,
Quelle est la période de la fonction f ?
Le spectre d’un signal est le diagramme obtenu avec :
– En abscisse, les entiers correspondants aux rangs des harmoniques (le fondamental = harmonique de rang 1) ;
– En ordonnée, les amplitudes An de chaque harmonique.
-
Rraphael3 dernière édition par
merci,
f=5HZ (sin)
f=10Hz(cos)Donc |C5| est l'hormonique vu=1?
-
Le fondamental ou harmonique de rang 1 a pour fréquence 5 et d'amplitude 2.
-
Rraphael3 dernière édition par
Bonjour,
reprenons depuis le début (Pour info nous avons un controle sur Fourier la semaine prochaine, alors que nous avons fait seulement 2 cours, beaucoup l'avait étudié avant mais pour moi c'est une grande première).Avec l'énoncé qui est plus haut,
2 sin(10 pi t) donne une fréquence de 5 car 2x5=10 c'est bien ça?
cos ( 20 pi t) donne une fréquence de 10 Hz car 2x10 = 20 c'est ça?Avec les résultats précédents on peut déduire les harmoniques qui sont des représentations graphiques?
Comment les calcules t'on et comment les positionner sur le graphe?En espèrant avoir été clair
-
Bonjour raphael3
Les fréquences sont correctes 5 et 10 Hz , f2 = 2 f1
donc deux harmoniques de rang 1 et 2.
Pour l'amplitude c'est (an2+bn2)\sqrt{(a_n^2+b_n^2)}(an2+bn2)
-
Rraphael3 dernière édition par
Merci Noemi,
Donc je vois pourquoi il y a 2 harmoniques.
9a veut dire qu'il faut creer un graphe avec deux raies une a 5HZ qui sera l'harmonique et une autre à 10Hz qui sera l'harmonique2.Par contre je n'ai plas compris l'amplitude: que représente rac? a ? b? et n?
à quoi cela sert?
-
Le signal peut s'écrire sous une forme générale :
a02\dfrac{a_0}{2}2a0 + ∑n=1∞\displaystyle\sum_{n=1}^{\infty}n=1∑∞(ancos(nx)+bnsin(nx))(a_ncos(nx)+b_nsin(nx))(ancos(nx)+bnsin(nx))Tu déduis à partir de l'écriture du signal les valeurs de ana_nan et bnb_nbn.
-
Rraphael3 dernière édition par
an= 2 et bn=1
sauf si il faut prendre les fréquences dans ce cas an=5 et bn=10
-
raphael3
Tu cherches l'amplitude pour chaque harmonique.
Pour le premier harmonique tu as que le sinus donc a5a_5a5 = 0 et b5b_5b5 = 2
donc A5A_5A5 = ....Même calcul pour le deuxième harmonique.
-
Rraphael3 dernière édition par
mais comment trouvez-vous 0 et 2?
Je dois être très bête mais je ne comprends pas, et je ne vois toujours pas en quoi l'implitude est nécessaire pour tracer le graphe?
-
La fonction peut s'écrire :
f(t) = 0 cos (10pit) + 2sin(10 pi t)+ cos(20 pi t) + 0 sin (20pit)
l'amplitude est aussi utile pour tracer le spectre.Pour le graphe de la fonction, tu peux faire une étude classique ou construire la fonction sinus et la fonction cosinus séparément puis faire la somme des deux fonctions sinusoïdales.
-
Rraphael3 dernière édition par
j'ai fait très peu de maths avant cette année et jamais de Fourier donc ça va très (trop) vite pour moi.
Maintenant je ne vois pas d'ou sors toute la formule.
Faut-il utiliser Euler ?
-
J'ai écrit la formule générale d'un signal dans un post précédent.
-
Rraphael3 dernière édition par
Oui je vois mais pourquoi noter 2 fois avec 0 puis 2 puis 0 puis 0
-
C'est suite à ta question sur le 0 et 2.
avec 10pit, tu retrouves a5a_5a5= 0 et b5b_5b5 = 2
avec 20pit, tu trouves a10a_{10}a10 = 1 et b10b_{10}b10 = 0
tu peux alors calculer les amplitudes.Les réponses pour les amplitudes de chaque élément de ce signal sont évidentes mais j'ai souhaité te donner la démarche dans le cas général.
-
Rraphael3 dernière édition par
je crois que j'ai compris :
10 pi t car sin (10 pi t)
a5=cos=0 b5=sin=2
-
Oui les ana_nan correspondent aux coefficients des cosinus et les bnb_nbn aux coefficients des sinus.
-
Rraphael3 dernière édition par raphael3
super j'ai compris il aura fallu le temps et je m'en excuse.
Une fois les résultats obtenus que aut-il faire?
-
Tu peux tracer le spectre et représenter la fonction sinus et la fonction cosinus.
-
Rraphael3 dernière édition par raphael3
vous avez mis plus haut, pour desinner le spectre en abscisse les entiers correspondants aux rangs des harmoniques quels sont ils ces entiers?
-
La fonction a deux harmoniques
un de fréquence 5 qui est le rang 1 (Le fondamental)
et un de fréquence 10 (5x2) donc de rang 2.
-
Rraphael3 dernière édition par
si j'ai bien compris le graphe devrait ressembler à:
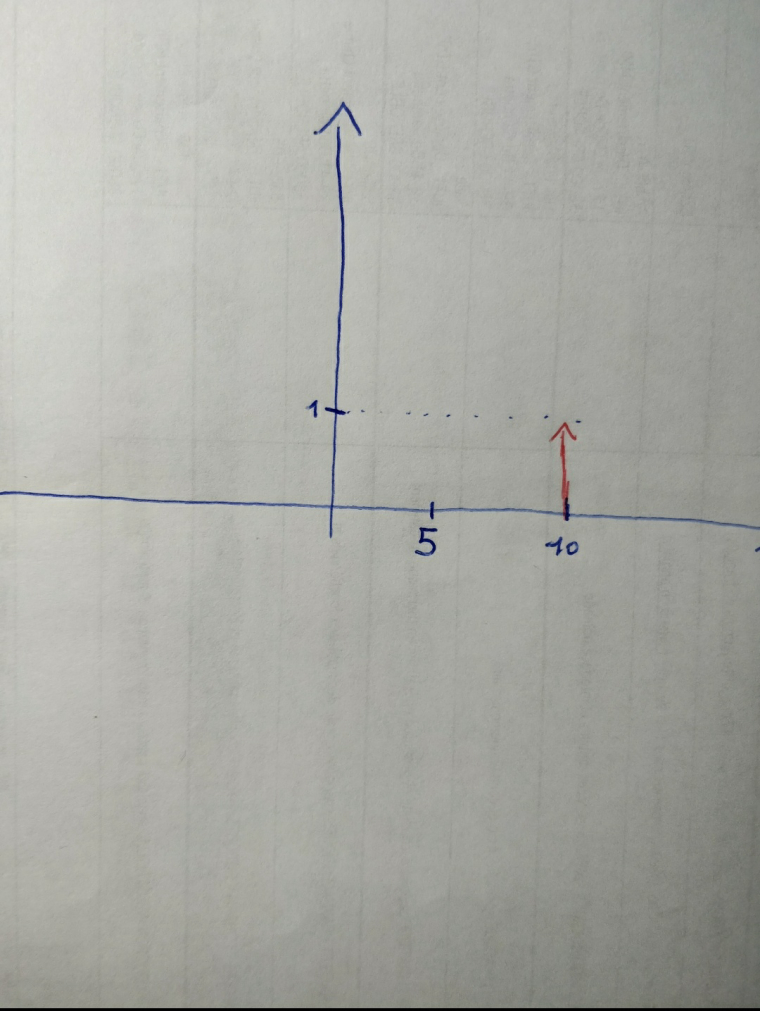
-
Non, Il manque le rang 1
Sur l'axe des abscisses 1 et 2
Pour le rang 1, la hauteur est de 2
Pour le rang 2, la hauteur est de 1.
-
Rraphael3 dernière édition par
Vu que vous vous aviez mis an pour les abscisses et an de 5 Hz est égal à 0 je pensais que la fléche était nul? donc il faut prende bn?
-
Pour rappel :
- En abscisse, les entiers correspondants aux rangs des harmoniques (le fondamental = harmonique de rang 1) ; Tu peux mettre 5 et 10
– En ordonnée, les amplitudes An de chaque harmonique.
Ne pas confondre amplitude An et ana_nan.
Utiliser la formule donnée pour calculer les amplitudes.
- En abscisse, les entiers correspondants aux rangs des harmoniques (le fondamental = harmonique de rang 1) ; Tu peux mettre 5 et 10
-
Rraphael3 dernière édition par
Oui c'est bon pour le graphe par contre j'ai vu plusieurs exemples sur internet ou il avait une symetrie entre le coté positif et negatif. Dois-je mettre les memes valeurs en négatifs?
-
raphael3,
Oui généralement on représente aussi le symétrique par rapport à l'axe des ordonnées.
-
Rraphael3 dernière édition par
Merci beaucoup pour votre aide précieuse