Probabilité - Couple de variables aléatoires
-
Rraphael_ dernière édition par
Bonjour,
J'ai commencé un nouvel exercice sur les variables aléatoires.
L'énoncé est:
Soient U et V deux variables de Bernoulli de même paramètre p. On pose X=U+V et Y=U-V- Déterminer la loi du couple (X,Y)
je fais un tableau (si j'ai bien compris )
X 0 1 2
Y
-1 0 0
0 0
1 0 0Par contre je n'arrive à placer que les 0 après je ne sais pas comment déterminer les valeurs.
- Les variables X et Y sont -elles indépendantes?
Je ne sais pas comment le déterminer néanmoins je pense que c'est lié à la question du dessus.
Merci
-
Rraphael_ dernière édition par
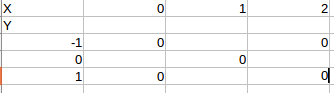
Le tableau sera peut-etre plus lisible comme ca, enfin je l'espère
-
Rraphael_ dernière édition par
Je viens de trouver un exercice qui explique les variables dépendantes. J'ai compris qu'il faut prouver que p(X n Y) = p(X) x p(Y)
Il y avait un exemple avec des cartes que j'ai compris mais dans ce cas je ne vois pas trop.
Peut etre faut il prendre U=V=1
Et faire les calcul donc X=2 et Y=0??
-
Bonjour raphael_
Construis un tableau des valeurs possibles de U et V, puis calcule les probabilités.
-
mtschoon dernière édition par mtschoon

Re-bonjour Raphael,
Je te suggère de commencer par voir ton cours les variables de Bernoulli de paramètre p . C'est indispensable.
Je te mets les cas
U=0 et V=0 donc X=U+V=0 et Y=U-V=0 probabilité (1-p)²
U=0 et V=1 donc X=U+V=1 et Y=U-V=-1 probabilité (1-p)p
U=1 et V=0 donc X=U+V=1 et Y=U-V=1 probabilité p(1-p)
U=1 et V=1 donc X=U+V=2 et Y=U-V=0 probabilité p²Tu fais un tableau où tu mets X/Y en colonne/ligne selon tes habitudes.
Tu remplis les cases avec les probabilité trouvées.
Les cases vides ont pour probabilité 0Ensuite, il te faudra compléter avec les probabilités marginales pour étudier l'indépendance ( ou la non-indépendance) de X et Y, mais, tu n'en es pas là.
-
mtschoon dernière édition par mtschoon

Bonjour Noemi .
Désolée, je n'avais pas vu ta réponse !
Plus précisément , ta réponse n'était pas là lorsque j'ai commencé à taper une explication..
-
Rraphael_ dernière édition par
Bonjour Noémi, bonjour Mtschoon,
Comme je le disais dans le premier problème demandé, il n'y a pas eu de cours sur les probabilités mais juste des séances de TD car tout le monde à étudié ce chapitre durant le bac et ou la prépa. Nous sommes seulement 2 à découvrir ce chapitre et on nous a gentiment dit de chercher comme des grands les cours associés sur internet. Ce que j'essaie de faire.
Mtschoon concernant votre réponse je ne comprends pas comment obtenir ces résultats.
Merci
-
raphael_ ,
Un lien vers un cours qui peut te fournir des éléments : https://www.normalesup.org/~glafon/carnot09/couples.pdf
Peut-être tu l'as déjà consulté.
-
mtschoon dernière édition par mtschoon

Pour la définition d'une variable aléatoire de Bernoulli, regarde ici, si tu as besoin :
https://fr.wikiversity.org/wiki/Variables_aléatoires_discrètes/Loi_de_Bernoulli
Cela s'applique dans ton exercice à U et à VJ'explicite un peu le principe de ton exercice.
U et V prenant les valeurs 0 et 1, je pense que tu comprends qu'il y a 4 cas pour (U,V] : (0,0] , (0,1], (1,0] ,(1,1]
Dans chacun de ces cas, tu déduis les valeurs de X et Y correspondantes
Dans chacun de ces cas, tu calcules la probabilité correspondante
exemples
U=0 a la probabilité (1- p), V=0 a la probabilité (1-p), donc "U=0 et V=0" a la probabilité (1−p)×(1−p)=(1−p)2(1-p)\times (1-p)=(1-p)^2(1−p)×(1−p)=(1−p)2U=0 a la probabilité (1-p), V=1 a la probabilité p, donc "U=0 et V=1" a la probabilité (1−p)×p(1-p)\times p(1−p)×p
Tu continues ainsi pour les deux autres cas.
Ensuite, pour faire le tableau (disposition pratique) relatif à (X,Y) je te mets un lien pour loi conjointe et lois marginales
Il y a les définitions écrites simplement et un exemple ( qui n'a rien à voir avec ton exercice) qui me parait clair et dont tu pourras t'inspirer.
http://www.bibmath.net/dico/index.php?action=affiche&quoi=./c/conjointe.htmlBon courage !
-
mtschoon dernière édition par mtschoon

Je te joins le tableau pour loi conjointe et lois marginales de ton exercice
Essaie de le comprendre , et bien sûr demande si ce n'est pas le cas.
(la loi conjointe est en noir et les lois marginales sont en rouge)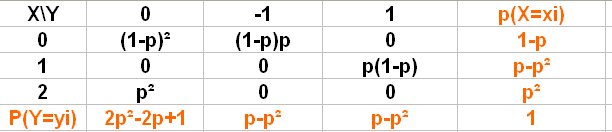
-
Rraphael_ dernière édition par
Bonsoir Noemi, Bonsoir Mtschoon,
Je suis vraiment étonné mais j'ai compris. Grâce à vos explications j'ai pu faire l'exercice seul et vérifier grâce à la correction que vous m'avez faite.
En tout cas Merci beaucoup je ne pensais pas que la loi de Bernoulli était si facile.Bonne soirée et à bientot.
-
mtschoon dernière édition par mtschoon

C'est parfait !

J'espère que tu as conclu sur la non-indépendance ou l'indépendance de X et Y.
Bonne soirée à toi .
-
Rraphael_ dernière édition par
pour la dépendance je sais qu'il faut prouver que P(X n Y) = p(X) x p(Y)
pour P(X n Y) je trouve {0,1+ par contre comment trouver p(X) et p(Y)?
-
mtschoon dernière édition par mtschoon

J'essaie de t'expliquer la notion d'indépendance et de non indépendance.
Comme indiqué dans le lien proposé, X et Y sont indépendantes si et seulement si pour tout xix_ixi et pour tout yjy_jyj
$\fbox{P(X=x_i,Y=y_j)=P(X=x_i)\times P(y_j)}$
Cela peut s'écrire
$\fbox{P((X=x_i)\cap (Y=y_j))=P(X=x_i)\times P(Y=y_j)}$S'il existe (au moins) une valeur de xix_ixiet une valeur de yjy_jyj pour lesquelles cette égalité est fausse, X et Y ne sont pas indépendantes.
Un exemple,
X=2 et Y=-1
En prenant l'intersection de la ligne horizontale correspondant à X=2 et la colonne verticale correspondant à Y=-1, tu trouves la case où il est indiqué 0 en noir
Cela veut dire P((X=2)∩(Y=−1))=0P((X=2) \cap (Y=-1))=0P((X=2)∩(Y=−1))=0 (loi conjointe)
En suivant la ligne horizontale correspondant à X=2, tu arrives à p² écrit en rouge
Cela veut dire P(X=2)=p2P(X=2)=p^2P(X=2)=p2 (loi marginale)
En suivant la colonne verticale correspondant à Y=-1, tu arrives à p-p² écrit en rouge
Cela veut dire P(Y=−1)=p−p2P(Y=-1)=p-p^2P(Y=−1)=p−p2 (loi marginale)Calcul :
P(X=2)×P(Y=−1)=p2(p−p2)P(X=2)\times P(Y=-1)=p^2(p-p^2)P(X=2)×P(Y=−1)=p2(p−p2)Il faut donc étudier p2(p−p2)=0p^2(p-p^2)=0p2(p−p2)=0
p2(p−p2)=0p^2(p-p^2)=0p2(p−p2)=0 <=>p2=0p^2=0p2=0 ou p−p2=0p-p^2=0p−p2=0 <=>p=0p=0p=0 ou p(1−p)=0p(1-p)=0p(1−p)=0 <=> p=0p=0p=0 ou p=1p=1p=1
Conclusion : dans le cas général 0<p<10 \lt p \lt 1 0<p<1 l'égalité est fausse. X et Y ne sont donc pas indépendantes.
Dans les cas extrêmes de p=0p=0p=0 et p=1p=1p=1, si tu analyses tout le tableau, tu dois trouver que X et Y sont indépendantes
Bon travail !
-
Rraphael_ dernière édition par
Bonsoir,
Je ne comprends pas comment vous trouvez ca:
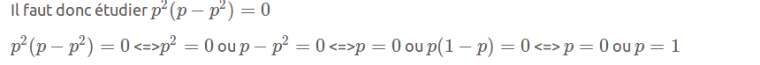
Merci beaucoup
-
mtschoon dernière édition par mtschoon

Bonjour,
Je ne sais pas précisément ce qui te gène : trouver l'équation ou la résoudre ...? ? ?
Dans le doute, j'essaie de détailler ces deux points.
-
Tu sais que :
P((X=2)∩(Y=−1))=0P((X=2) \cap (Y=-1))= 0P((X=2)∩(Y=−1))=0
P(X=2)=p2P(X=2)=p^2P(X=2)=p2
P(Y=−1)=p−p2P(Y=-1)=p-p^2P(Y=−1)=p−p2
Donc:
P(X=2)×P(Y=−1)=p2(p−p2)P(X=2)\times P(Y=-1)=p^2(p-p^2)P(X=2)×P(Y=−1)=p2(p−p2)
Pour l'indépendance, la question est :
$\fbox{P(X=2)\times P(Y=-1)= P((X=2) \cap (Y=-1))}$ ?
En remplaçant chaque probabilité par sa valeur, la question devient :
$\fbox{p^2(p-p^2)=0}$ ? -
Résolution de cette équation $\fbox{p^2(p-p^2)=0}$
Pour qu'un produit de facteur soit nul, il faut et il suffit qu'un des facteurs soit nul
Donc deux cas : p2=0p^2=0p2=0 ou p−p2=0p-p^2=0p−p2=0
1er cas p2=0p^2=0p2=0 <=> p=0\fbox{p=0}p=0
2ème cas : p−p2=0p-p^2=0p−p2=0
en factorisant : p(1−p)=0p(1-p)=0p(1−p)=0
En utilisant encore une fois la propriété "Pour qu'un produit de facteur soit nul, il faut et il suffit qu'un des facteurs soit nul", on obtient
p=0\fbox{p=0}p=0 ou 1-p=0\fbox{1-p=0}1-p=0
en transposant 1−p=01-p=01−p=0 <=> 1=p1=p1=p <=> p=1\fbox{p=1}p=1Les deux valeurs de p pour lesquelles X et Y sont indépendantes sont donc 0 et 1
Vu que par définition 0≤p≤10 \le p \le 10≤p≤1, tu déduis que pour 0<p<10 \lt p\lt 10<p<1 X et Y ne sont pas indépendantes (on peut dire bien sûr que X et Y sont dépendantes, mais comme l' indépendance est la propriété importante, on utilise plutôt l'expression "ne sont pas indépendantes".
-