Dérivée-Tangente à une parabole
-
Ccedren dernière édition par mtschoon
Bonjour, j'ai un devoir maison à rendre sur les dérivé, on vient de commencer la leçon et je ne sais pas comment faire, voici le sujet:
Soit P la parabole d'équation y=x au carré dans un repère orthonormal du plan.
- Soit a un nombre quelconque. Établir une équation de la tangente (T) à P au point M d'abscisse a différente de 0. On écrira cette équation sous la forme y=mx+p, où m et p sont exprimés en fonction de a.
- (T) coupe l'axe des abscisses en N et l'axe des ordonnées en Q. Montrer que N est le milieu du segment MQ.
- En déduire une méthode géométrique de construction de la tangente (T)
Je ne sais pas comment commencer à répondre à ces questions, pouvez-vous m'aider, merci d'avance.
-
mtschoon dernière édition par

Bonjour,
Piste pour démarrer,
f(x)=x2f(x)=x^2f(x)=x2
Regarde ton cours.
Tu dois y trouver l'équation d'une tangente (T)
y=f′(a)(x−a)+f(a)y=f'(a)(x-a)+f(a)y=f′(a)(x−a)+f(a)f(x)=x2f(x)=x^2f(x)=x2 doncf′(x)=2xf'(x)=2xf′(x)=2x
Pour x=a, f(a)=a2f(a)=a^2f(a)=a2 et f′(a)=2af'(a)=2af′(a)=2aTu remplaces dans l'équation de (T) et tu développes pour mettre l'équation sous la forme demandée.
Essaie de poursuivre.
Tiens nous au courant de tes réponses si besoin.
-
mtschoon dernière édition par

Un graphique, pour t'éclairer
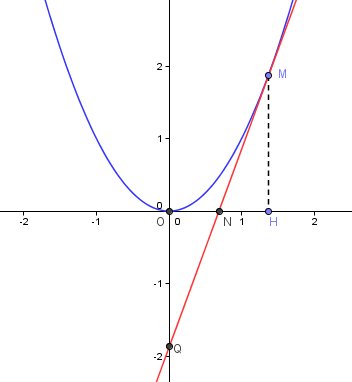
-
Ccedren dernière édition par mtschoon
@mtschoon rebonjour, merci, pour la question 1 j'ai trouvé:
y=2a x (x-a) + a au carré
développé, ça me donne:
y=2ax - 3a²
je ne suis pas sûre de ma réponse, est ce que c'est bien ça?
-
mtschoon dernière édition par

Tu as fait une erreur de signe.
y=2ax-2a²+a²=....
-
mtschoon dernière édition par mtschoon

J'espère que tu as rectifié l'erreur sur l'équation de la tangente qui doit être y=2ax-a²
Pistes pour la suite :
Pour N : y=0
Tu remplaces y par 0 dans l'équation de (T) et tu trouves xPour Q : x=0
Tu remplaces x par 0 dans l'équation de (T) et tu trouves yPour montrer que N est le milieu du segment [M] :
Tu vérifies que
xN=xM+xQ2x_N=\frac{x_M+x_Q}{2}xN=2xM+xQ et yN=yM+yQ2y_N=\frac{y_M+y_Q}{2}yN=2yM+yQBons calculs.
.